2.1 支柱一最低资本规定
由于银行提供的信贷总量以及借款者的还款能力会随着宏观经济形势而变化,银行资产组合的信用风险也会随着经济周期而变化。如果对资本的监管旨在减少个别银行倒闭所带来的潜在社会成本,那么它就应该随着倒闭的可能性而变化,这就意味着要随着银行的相对风险而变化[4]。1988年《巴塞尔资本协议》对不同国家最低资本规定的实施提供了方法,但是并未考虑到随着时间推移,银行信贷敞口所发生的相对风险变化所导致的单一信用风险资本规定变化。由此,提高对信用风险资本规定的风险敏感性,同时保持对加权资产8%的最低资本充足率要求,成为了《巴塞尔新资本协议》的首要目的。
在《巴塞尔新资本协议》的支柱一下,这一目的是通过规定两种计算方法来计算信用风险的资本规定而实现的。《巴塞尔资本协议》中的标准法为公司、银行及主权债权分配了不同的风险权重。相比之下,《巴塞尔新资本协议》的标准法根据外部评级的变化而改变信用风险的权重,更能体现风险敏感性。在《巴塞尔新资本协议》内部评级法的要求下,更高的风险敏感性来自于银行对每个头寸的风险构成进行估计。内部评级法也有两种选择。根据内部评级初级法,银行需要估计违约概率(PD)和违约风险暴露(EAD)。采用高级法的银行还需估计期限和违约损失率(LGD)(根据初级法规定水平设定)。这些措施原则上是否会在支柱一资本规定下导致顺周期性,取决于两种方法的关键输入参数,即随经济周期变化的外部评级和对风险构成的估计。现实中是否会引起顺周期性的资本规定,取决于实施支柱一时的具体方法。在回顾潜在的顺周期性资本规定增加与支柱一监管资本规定之间的实证研究文献之前,我们先考虑两个问题。
2.1.1 输入参数的潜在周期性
标准法
标准法使用外部评级信息来确定主权、银行及公司债权的风险权重[5]。与《巴塞尔资本协议》只按债权种类给予风险权重的方法相比,标准法通过多重评价体系使得风险敏感性得到提高(主权债权及银行债权有六级,公司债权有五级[6])。这些安排是否会在最低监管资本规定下导致更高的顺周期性,取决于外部评级是否随周期而变动。
原则上,外部信用评级自称是在“跨越周期”的基础上进行衡量的[7]。然而,Segoviano和Lowe(2002年)研究发现,评级迁移矩阵(指示评级结果变化的可能性)并未随着周期的变化而变化(见Lowe,2002年)。Amato和Furfine(2003年)发现,当一般评级相对稳定的时候,如果作出调整,则公司的状况往往会作出过度的反应。事实上,这种过度反应与经济总体情况是正相关的。这些证据似乎暗示着,在标准法下,使用细分的风险评价体系,会使得监管资本规定的变化导致更高的周期性。
内部评级法
内部评级法下,一项贷款的最低监管资本规定是以下指标的函数:
·违约概率(PD);
·违约风险暴露(EAD);
·违约损失率(LGD);
·期限(M);
·资产价值与普通风险因素相关的系数(p)[8]。
这些因素对于决定监管资本变化的重要作用,已经引起学术界广泛讨论其周期行为[9]。这些研究有如下的关键特点。
对于违约概率,《巴塞尔新资本协议》允许银行使用三种估算技术[10]:
·内部违约经验:与使用外部评级方法一样,由于等级影响及传导影响,这种方法也会导致对违约概率的估计产生周期性。等级影响下,平均违约率在单个信用级别中变动,而在传导影响下却在信用级别之间变动。等级影响是否会导致违约概率产生潜在的周期性,取决于估计的时期。对时期作出调整可以缓解其带来的周期性,例如《巴塞尔新资本协议》即要求使用长期的违约概率估计值。事实上,鉴于这一原因,Corcóstegui等人(2003年)在对1993~2000年西班牙私人非金融部门贷款的数据进行内部评级模拟分析时,认为传导影响实为二者中更重要的。
·映射外部数据:将内部评级与外部评级相映射,然后使用外部评级数据中的违约概率。鉴于外部数据存在不同程度的不完善性,这种方法同标准法一样也存在导致周期性的问题。
·统计违约模型:人们已经开发了多种统计模型,并将其应用到银行对违约概率的估计中(见Allen和Saunders,2003年;Borio等人,2001年)。以市场价格为基础、使用莫顿期权定价方式的模型,认为违约概率随着公司负债率的提高、权益价格波动性的增加而上升,随着权益价格的上升而下降。这些模型,例如KMV模型,可能通过资产价格的顺周期性而导致对违约概率的估计产生周期性。其他的模型,如信贷矩阵,使用评级矩阵作为在险价值的输入数据来计算违约概率,这就又回到了上面我们讨论评级矩阵的周期性问题。一些模型,如CreditPortfolio View及CreditRisk+模型,也嵌入了周期性的变量。这样一来,使用统计模型基于一年期进行的估计,以及为作出长期估计而进行的调整,通常会导致违约概率的估计带有周期性(Borio等人,2001年)。
最低资本要求的公式里的其他参数也显现出了一些周期性影响。例如,Gordy和Howells(2004年)发现,尽管证据有限,但期限在经济衰退时呈下降趋势。Allen和Saunders(2003年)则详细指出,违约风险暴露也同样存在有趣的周期性。而在衰退时,贷款承诺也同样适用。同样,资产价值与描述经济状况的风险因素的相关关系也有周期性特征。Lopez(2004年)发现,对于美国、欧盟和日本的资产组合,这种相关性是违约概率的负函数(在《巴塞尔新资本协议》的框架下),是资产规模的正函数。由于违约概率在经济好转时的下降程度不同,资产价值的相关关系也同样是周期性的。
违约损失率周期性的证据更复杂。Altman等人(2002年)发现,证券的加权违约损失率在衰退时更高。Acharya等人(2004年)最近的研究证实了这一观点。他们发现,行业情况是影响违约损失率的主要因素,违约债权的总回收率与总违约率和违约债券的总供给负相关,一旦考虑到行业情况时,这些总量变量就变得毫无意义了。然而,在衰退时期,许多行业都处于弱势,而银行对很多行业均有风险敞口,其违约损失率就会经历周期性变动。Gordy和Howells(2004年)指出,基于债券数据的研究并不能代表贷款组合的违约损失率。如果债务人违反合约对财务比率的要求,贷款合约就允许银行重新谈判贷款条件。这说明重新谈判也许包含增加抵押物的条件,意味着对于贷款而言,如果违约概率上升,则违约损失率会下降,也就是说违约损失率的周期性会被违约概率的估计所抵消。然而,这一特征也许只针对特定的银行及法律框架[11]。
2.1.2 支柱一的方法
支柱一所给出的方法相当多,占据了巴塞尔委员会2004年协议正文的150多页,而支柱二只占15页,支柱三只占25页。现有资料已经说明,在计算最低资本要求时,对上述参数在不同时间的估计会产生周期性,而能够起到抵消作用的方法,就是对参数在更长的时间内进行估计。《巴塞尔新资本协议》也提倡使用这一方法,例如:
·违约概率估计——评估的时间:“评级时考虑的经济状况,必须与当前状况以及在经济周期内各自行业/地区可能发生的状况一致。”(第415段)。“为了估计违约概率,无论银行使用外部数据、内部数据、汇集数据,或是三种数据来源的结合,每种数据源的历史观察期至少要有5年。如果某种数据来源有较长的观察期,且数据有意义,必须采用更长的观察期。”(第463段)。标准法也有同样要求。
·自己估计违约损失率:对于公司、主权和银行的风险暴露,“估计违约损失率必须参考最短的数据观察期。在理想情况下,数据观察期至少应该涵盖一个完整经济周期,而且任何情况下,至少一个数据来源的观察期不应该少于7年。如果任何一个数据来源的观察期跨度更长,且数据有意义,应该采用较长的观察期。”(第472段)
·自己估计违约风险暴露:对于公司、主权和银行风险暴露观察期的最短要求与自己估计违约损失率是相同的。此外,“对于违约风险暴露在经济周期不稳定时期的贷款,如果经济低迷时期的违约风险暴露比长期的平均数更保守,银行必须使用适合经济低迷时期的违约风险暴露。”(第475段)
·内部评估的验证:“银行必须证明,定量的检测方法和其他验证方法不会随经济周期发生系统性变化。”(第503段)
在全文强调的TTC方法下,由于计算最低资本要求而产生的周期性很难完全消除。首先,存在描述的时期是否与经济周期长短一致的问题。其次,TTC方法是否被行业采用也是个问题。许多现存的体系倾向于使用PIT,市场上的消息也说商业银行在《巴塞尔新资本协议》的要求下也仍然使用PIT[12]。作为反应,金融服务局(FSA)文件指出,由于在巴塞尔方法及现存实践之间存在差距,并且确有其他方法来处理周期性,现有的PIT方法至少在过渡期可以短期适用(参见第3.247段,金融服务局,2003年)。
2.1.3 对最低监管资本要求引起的顺周期性的估计
《巴塞尔新资本协议》倡导并要求使用实证方法,以此来估计支柱一最低资本要求引起潜在的增加的顺周期性。计算资本规定的内部评级法具有更高的风险敏感度和更大的变动,因此成为研究的重点[13]。这些研究的大致观点就是,在内部评级法下,最低资本规定确实引起了顺周期性的显著增加。例如Gordy和Howells(2004年)发现,新方法平均引起资本规定的变动性增加0.1~0.26(依模拟方法不同而有变化)。为了给出在经济下滑时资本规定增加的程度,Kashyap和Stein(2003年,2004年)估计,在1998~2002年,如果使用KMV模型,则投资级资产组合的资本规定增加了70%~90%,如果使用标准普尔的评级模型来计算违约概率,则会引起资本规定增加35%。这些数据与其他研究得出的结论一致(表1再现了Kashyap和Stein的研究结论)。
这些研究也指出,质量越高的信贷,其资本要求的波动性就越大。因为这类信贷评级下降的空间比较大,并且有着更陡峭的风险曲线。在2.1.1部分的讨论中,违约概率方法同样起到了重要作用。对于投资级组合,专用于PIT方法的KMV模型会得出比基于评级的方法更强的顺周期性,而对于非投资级的组合则要少(参见Kashyap和Stein,2004年;Catarineu-Rabell等人,2003年)。
尽管大量研究均得出了一致结论,但是鉴于该问题的复杂性,这些研究也存在一些警示。最重要的是,卢卡斯批判是否适用。这对于基于历史数据的研究(例如Kashyap和Stein,2003年;Segoviano和Lowe,2002年;Corcóstegui等人,2003年)及模拟分析(例如Gordy和Howells,2004年;Kashyap和Stein,2003年;Peura和Jokivuolle,2004年)都适用。此外,在解释结果的时候,也必须考虑到一些特殊的有趣方法。
首要问题就是在模拟中假定的资产组合管理方法。Gordy和Howells(2004年)有力地说明了这对估计结果会有影响。例如,周期投资法则(银行根据“逆风向原则”贷款)导致资本要求的波动性较低,且与消极组合相比具有更低的平均值[14]。后一种方法,例如Kashyap和Stein(2004年)所使用的那样,假定新贷款不会改变组合的评级分布。但是,当经济下行时,银行是否可能一次性地吸引高信用级别的借款人呢?古德哈特(2004年)发现,在Gordy和Howells的反应里暗示着,这些假定也许是美国金融市场发展水平的特征。在美国,具有良好信用品质的大型公司在繁荣时使用债券和商业票据融资。然而,当市场趋于下行时,这些公司就会寻求银行提供支持性融资。很明显,对于并不具有这一特征的欠发达市场,假定这一投资规则并不合适。
表1 对资本要求周期性的若干研究
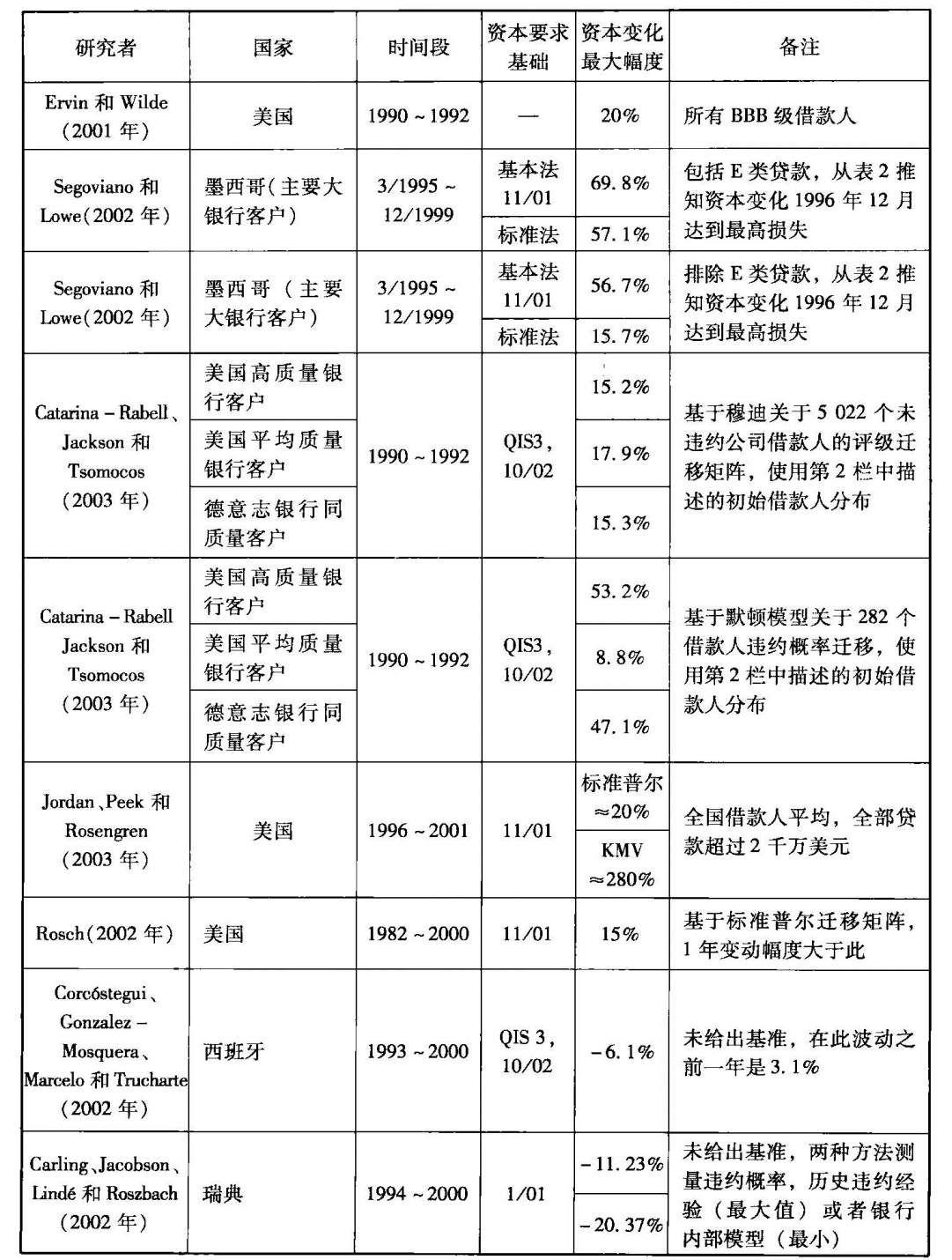
资料来源:选自Kashyap和Stein(2003年)表4。
尽管一些研究使用了实际贷款数据,例如,Corcóstegui等人(2003年);Kashyap和Stein(2003年);Segoviano和Lowe(2002年),但许多研究还是使用债券评级数据来得出违约概率。这又产生了一个问题,即鉴于融资特点的不同,这些结果在多大程度上能够适用于贷款。模型间其他的变动并无多大价值,如《巴塞尔新资本协议》使用的确切公式、不同样本、填补空白观察期和偏差的方法。对后者而言,分析《巴塞尔新资本协议》带来的顺周期性问题的一致认同的方法中应排除违约贷款。
