2.2.2 PP检验
2026年01月14日
2.2.2 PP检验
ADF检验在一定程度上修正了残差中的序列相关问题,但滞后期的确定仍是一个问题,因为过长的滞后期会损失样本信息。Philips与Perren(1987,1988)提出了一种非参数检验方法:PP检验,其基本思想是通过附加一个修正因子来完善单位根检验。王少平(2002)研究了残差在动态设定下PP检验的分布,得出结论:当残差为i.i.d时,PP检验退化为DF检验;若残差为一般动态设定,该检验的分布与残差为i.i.d的DF分布相同(称之为标准DF分布,即式(2-9)(2-10),这说明PP检验从理论上修正了自相关和异方差问题。
PP检验的三个检验方程与DF检验相同,分别为:(2-3a),(2-3b),(2-3c)。
检验是否存在单位根则是检验假设:H0:ρ=1;H1:ρ﹤1。
检验统计量为:(https://www.daowen.com)
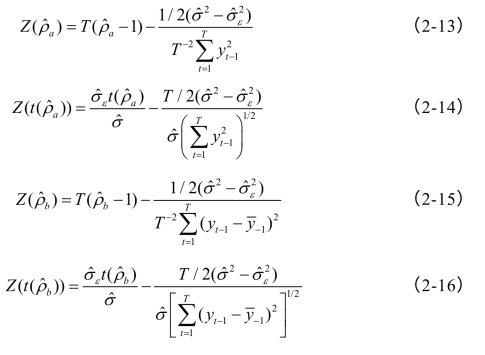
这里![]() 为εt的方差,则
为εt的方差,则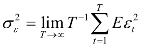 ,其一致估计为:
,其一致估计为:![]()
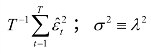 为εt的长期方差,记部分和
为εt的长期方差,记部分和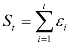 ,则
,则![]() ,其一致估计需使用非参数核估计[2],
,其一致估计需使用非参数核估计[2],![]() 。
。
在原假设成立的条件下,PP检验统计量与DF检验统计量有相同的分布。
