2.2.3　KPSS检验

2.2.3　KPSS检验

Kwiathowski，Phillips，Schmidt与Shin（1992）提出了KPSS检验，此检验用以判别平稳序列I(0)与非平稳序列I(1)。KPSS检验的基本思想是对从待检验序列中剔除截距项和趋势项后的序列构造LM统计量。

KPSS检验的回归方程为：

对该回归方程作OLS估计可得为剔除截距和趋势项后的序列，KPSS检验即检验该序列是否存在单位根以判定原序列{yt}是否存在单位根。

检验的原假设H0:序列{yt}是（趋势）平稳的；备择假设H1:序列{yt}是非平稳的。

当序列{ut}不存在序列相关时，检验统计量为：

其中，部分和为ut的方差σ2的一致估计，可用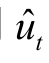的方差近似：。

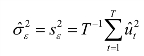而当序列{ut}存在序列相关时，检验统计量则为：(https://www.daowen.com)

其中为ut的长期方差σ2的一致估计，其近似值与PP检验分析相同。

在原假设成立的条件下，当为水平平稳情形（δ＝0），则当T→∞时，有：

当为趋势平稳情形（δ≠0），则当T→∞时，有：

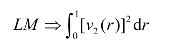
其中v2(r)为二阶布朗桥^[3]。

实际应用时，可利用各统计量的经验分布临界值表和响应面函数。