7.4.1 非线性函数逼近的仿真研究
2026年01月14日
7.4.1 非线性函数逼近的仿真研究
选取研究文献中给出的几类函数,应用BP-LM改进算法、BP-LM剪枝算法、GA-BP-LM改进算法、2层GA-BP-LM改进算法、径向基RBF-RPCL-LAF学习算法以及小波WNN-LM改进算法,进一步考察两隐层的BP网络的改进LM算法,迭代3000次,相应结果列表7-1如下:
表7-1 三种非线性函数的不同神经网络方法的逼近效果
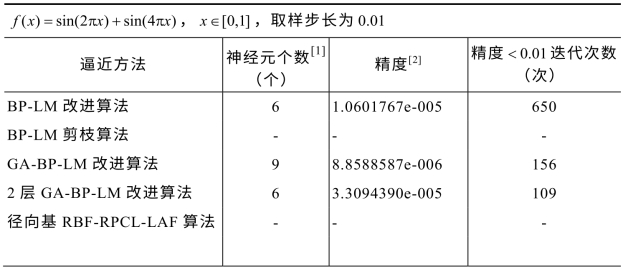
[1]一般地,逼近精度会随神经元个数的增加先减少后增加,故本书给出的是精度最高时对应的神经元个数。
[2]本书精度计算所用公式为: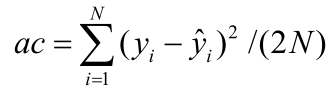 。
。
续表
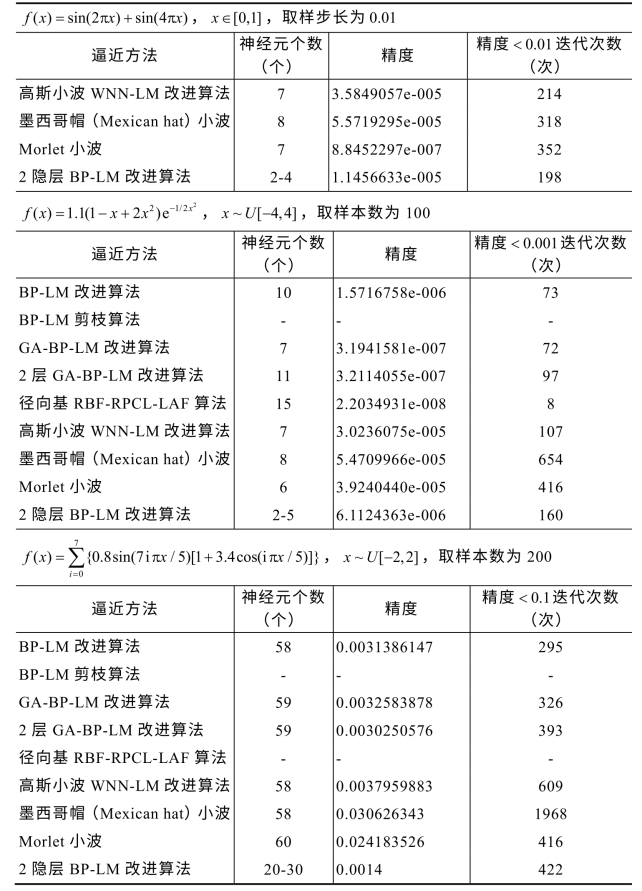 (https://www.daowen.com)
(https://www.daowen.com)
由表7-1可得如下几个方面的结论:
(1)基于BP-LM的剪枝算法,对剪枝的控制难度,使得其应用存在较大的问题,而径向基神经网络的泛化能力具有明显缺陷,中心的选择是其难点。
(2)基于BP-LM改进算法的神经网络与小波神经网络都具有很强的非线性函数逼近能力,并且对于不同的函数都具有很强的泛化能力,可以结合遗传算法保证其稳健性。当然,多层遗传算法的种群增加和运行代数GA的大小会使得算法运行时间过长。
(3)基于两隐层的BP-LM算法与单隐层神经网络相比,其逼近精度没有明显的区别,一样具有很强的泛化能力,隐层神经元总个数一般而言少于单隐层神经元个数,并可以结合遗传算法以保证其稳健性,但是较单隐层具有更多的估计参数,同时也存在运行时间过长的问题。
上述研究是基于确定性的非线性函数关系进行仿真模拟的,而当输入的样本数据序列Xt和目标样本数据序列yt都为随机数列时,对于其可能存在的非线性函数关系,由于受到随机因素的干扰,则会出现过度拟合或拟合不足的现象,则需要重新审视比较各类神经网络的拟合能力。
