3.3 Monte Carlo仿真模拟
Lee、White与Granger（1993）对代表各种平稳非线性情况的模型中产生的两组单变量序列应用神经网络法（NEURAL）（法1），KEENAN（法2）、TSAY（法3）、WHITE（法4）、Mcleod-Li（ML）（法5）、RESET（法6）以及DBS（法7）等检验方法进行MC模拟，结果如表3-1所示：
表3-1 各检验方法对不同模型的非线性存在性检验效果
续表
注：表中所列的是样本容量为200的功效或水平扭曲，*，**，***分别表示大于60%，80%，95%的功效或者10%，5%，1%的水平扭曲，由于各检验所用5%处模拟临界值和渐近临界值（组1和组3为模型1的模拟值，组2为模型9的模拟值，重复次数为6000次）的效果相近，故不分开表述。表中结果来源为Lee，White与Granger（1993）的研究成果。
由表3-1可见，Lee、White与Granger（1993）有如下结论：Mcleod-Li的检验效果较其他检验效果都差，BDS检验仅对双线性模型功效较强，所用神经网络检验除对双线性模型检验效果差之外，对其他模型则相近于或优于标准检验。由此可见，神经网络检验方法具有较强的应用价值。
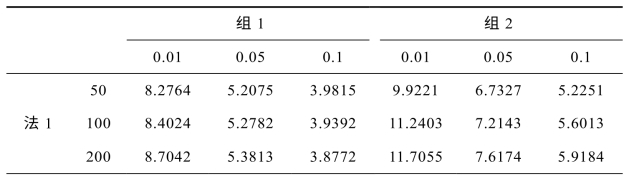
本书则进一步研究BP加强型神经网络和小波神经网络进行上述模型被忽略的非线性检验的效果，使用基于改进的带动量的LM算法，考虑第7章7.3.5所讨论的线性加强S型BP神经网络（法1）与高斯小波（法2）、墨西哥帽小波（法3）与Morlet小波神经网络（法4）。按照Lee、White与Granger（1993）的思路，这里考虑神经元个数组1取q＝10，组2取q＝20；对于组1取q*＝2，组2取q*＝3；考虑样本容量分别为50，100，200的模拟结果如表3-2所示。
表3-2 各线性加强神经网络不同样本容量在1%，5%及10%显著性水平下的临界值
续表
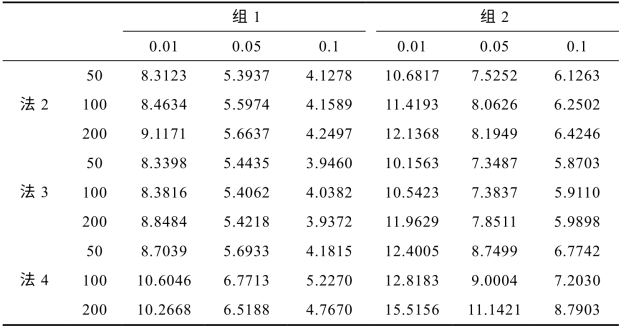
注：组1、组2分别在1%，5%及10%显著性水平下的渐近临界值为9.210，5.991，4.605以及11.341，7.815，6.251。本表为重复6000次得到的数值。
由表3-2可知，线性加强S型BP神经网络（法1）与高斯小波（法2）、墨西哥帽小波（法3）等两加强型小波神经网络方法的临界值与渐近临界值相近，可用于被忽略的非线性存在性检验。