6.3.3　记录数统计量RCC和RCCCD的临界值及其响应面函数

6.3.3　记录数统计量RCC和RCC CD的临界值及其响应面函数

1.记录数统计量的临界值表

利用Gauss编程，MC模拟生成两独立的I(1)DGP序列，重复10000次生成随机游走数据。以T=100，500为例，RCC检验统计量与RCCCD检验统计量的频率分布如图6-6所示。

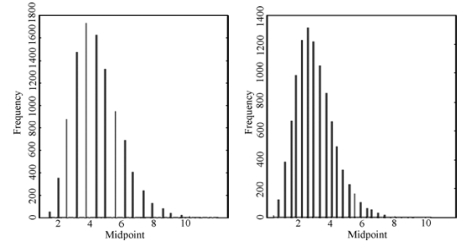
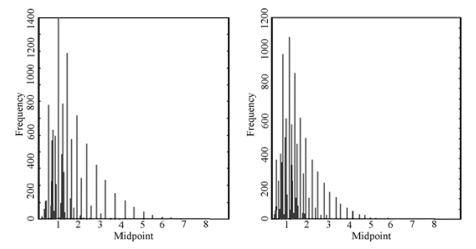
图6-6　T=100，500时，记录数统计量RCC（左），RCCCD（右）的频率分布

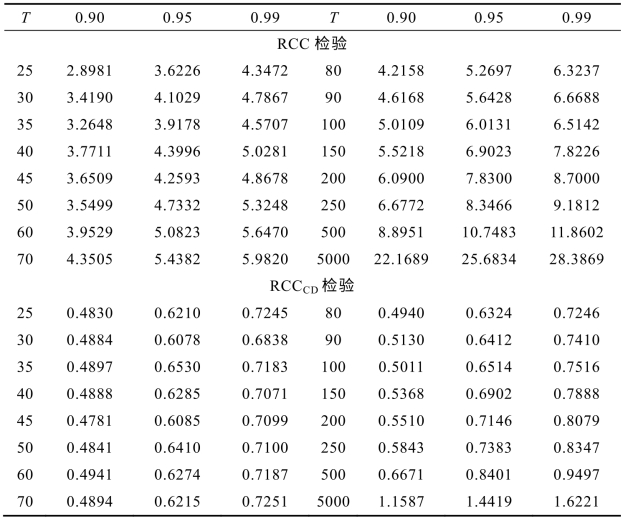
其临界值表如表6-5所示。

表6-5　两种记录数检验的临界值

2.响应面函数

本书进一步计算了T从25到5000共114个样本容量的两记录数统计量RCC与RCCCD的临界值，其与样本容量T的变化图如图6-7所示。

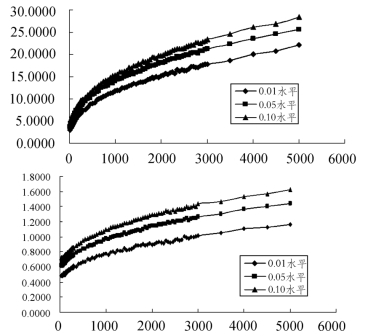
图6-7　记录数统计量RCC（上），RCCCD（下）在显著性水平0.01，0.05，0.10对样本量T的变化图

由图6-7可见，两统计量都随样本容量的增加而增加，但并未渐近趋于平稳，故而对于不同样本量T，其临界值响应面函数由回归模型确定，如表6-6所示。

表6-6　记录数统计量RCC，RCCCD的响应面函数及其估计

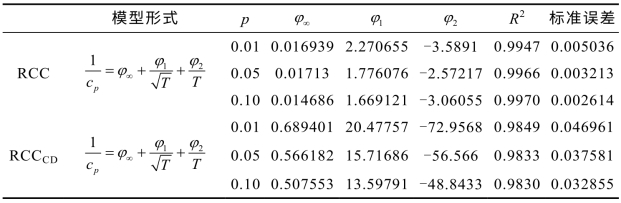
注：表中各记录数统计量响应面函数进行回归所用数据为MC模拟得到，重复次数10000次，T的取值从25到5000共114个样本点。