6.2.2　协整关系中存在非线性的秩检验

6.2.2　协整关系中存在非线性的秩检验

上述协整的秩检验方法，虽然能够检验出变量间的非线性协整关系，但并不能保证所检验出的协整关系就是非线性的。也就是说，上述秩检验方法检测出的协整关系，可能是线性协整关系，也可能是非线性协整关系。因此，对于用上述方法已经检验出的协整关系，还需要进一步检验该协整关系是否为非线性。

对于两变量的情形，Breitung（2001）假设非平稳变量xt和yt两者间的非线性关系为：

其中ut为白噪声，且ut～N(0,σ2)。在无非线性关系的原假设下，对于所有的t，有f*(xt)＝0。在原假设下，用OLS方法对式（6-7）进行估计，可得回归残差序列为：

再用OLS方法估计此残差序列对变量xt及其秩的辅助回归方程，得：

则此辅助回归方程的拉格朗日乘子（LM）得分统计量TR2就可用来检验xt和yt间没有非线性关系的原假设。Breitung（2001）证明了得分检验统计量TR2～χ2(1)。

对于多变量的情形，给定k＋1个变量(yt,x1t,x2t,…,xkt)，可假设潜在的非线性模型为：

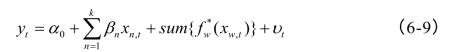
式中为对集合中元素的一个、多个或全部求和。考虑到可能出现的自相关性，可用OLS建立如下的回归方程：

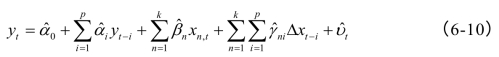
然后，用式（6-10）的残差序列再估计辅助回归方程：

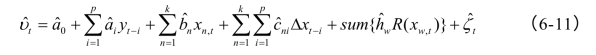
在联合原假设成立的条件下，辅助回归式（6-11）的拉格朗日乘子得分统计量TR2～χ2(m)，m为中元素的个数，T为回归模型（6-11）中的样本容量。若TR2统计量显著，则意味着至少有一个非零，从而可以认为协整关系中存在非线性。