3.2.3 BDS检验
2026年01月14日
3.2.3 BDS检验
Brock、Dechert 和Scheinkman(1987)在研究混沌存在性检验过程中利用关联积分提出BDS检验。研究表明,该检验适合于鉴别通常的随机非线性。
考虑统计量:
![]()
其原假设为{H0:xt是i.i.d的}。在原假设成立的条件下,![]() 渐近服从正态分布,其均值为0,方差为:
渐近服从正态分布,其均值为0,方差为:
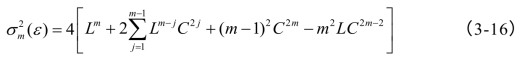
其中![]() ,而C1(ε)为C的相合估计,L的一致估计可以表为:(https://www.daowen.com)
,而C1(ε)为C的相合估计,L的一致估计可以表为:(https://www.daowen.com)
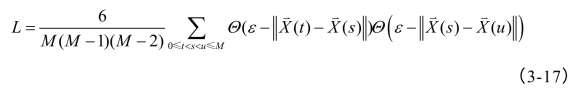
从而BDS统计量可定义为:
![]()
Liu、Granger和Heller(1992)研究表明,将独立同分布作为原假设,当数据呈确定性混沌时,BDS检验可以正确拒绝原假设,其在识别线性随机过程和非线性随机过程时具有一定的作用。
BDS主要用于对随机或确定性进行非线性检验,故而实践中在进行BDS检验时有必要将序列中的线性部分消除,而当检验拒绝原假设时,则意味着数据中“非线性”的存在。
