5.1.3 推广的KPSS检验法
2026年01月14日
5.1.3 推广的KPSS检验法
Kwiathowski、Phillips、Schmidt与Shin(1992)提出的KPSS检验主要应用于线性时间序列的平稳性检验,Lee与Schmidt(1996)推广了KPSS检验,用以区分短记忆与长记忆时间序列。其基本思想如下:
对于时间序列{xt},考虑其分整表达式:
![]()
这里{ut}是短记忆序列,满足![]() ,且有xt=(1-L)-dut,d∈(-0.5,0.5)。记部分和过程
,且有xt=(1-L)-dut,d∈(-0.5,0.5)。记部分和过程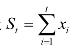 ,其方差为
,其方差为![]() 。
。
对于上述分数维过程,Sowell(1990)证明,其部分和的方差为:
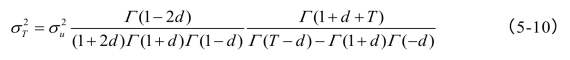
当T→∞,有:
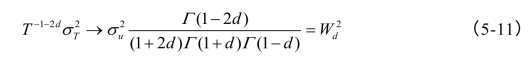 (https://www.daowen.com)
(https://www.daowen.com)
进一步,对于r∈[0,1]有:
![]()
这里Wd(r)为分数维布朗运动。
由式(5-11)、(5-12)有:
![]()
那么,设定原假设H0:{xt}为短记忆序列,备择假设H1:{xt}为长记忆序列,则如果{xt}是分整的即长记忆的,则{St}为Op(Td+0.5);否则,如果{xt}是短记忆的,则{St}为Op(T0.5)。
上述检验临界值需通过MC方法实现,Lee与Schmidt(1996)的研究表明,推广的KPSS检验的功效与修正的R/S检验相近。
