7.4.3 非线性协整检验与估计的仿真设计
对于非线性非平稳时间序列，Granger和Hallman（1991）指出，虽然短期时间序列的非线性关系受到随机干扰项的影响而难以检验和估计，但是长期均衡关系则可用ACE算法进行估计；张世英等（1999，2004，2005）利用神经网络进行非线性协整系统的建模和检验，为多变量之间非线性均衡关系的研究提供理论支持，本书进行研究发现，神经网络方法相对于ACE算法更具有对未知非线性函数的估计优势。然而，利用神经网络进行非线性协整的检验与估计，张喜彬、孙青华、张世英（1999）提出将所有时间序列变量作为输入变量，考察更一般的各序列间的隐函数形式，用常数作为输出训练神经网络，本书MC认为可能存在过度拟合问题而值得商榷。因此本书讨论具有显性非线性结构的情形。
由式（7-9），利用神经网络方法估计其非线性函数，得到残差为：那么，由神经网络的逼近理论，单隐层神经网络即可析取变量间的非线性结构，则可进一步应用常规的单位根检验方法如ADF检验、SPSS检验及PP检验来确定残差序列是否平稳。若是非平稳的，则前述检验方法得到的结论有待进一步研究；若不存在单位根，则说明残差序列是平稳的，那么可以认为，原时间变量间存在非线性协整关系，而神经网络估计的函数形式可以作为非线性结构的一种近似估计量，从而可以进一步展开各种分析和预测研究。
考虑单调变换与非单调变换的非线性函数的情形，现产生如下三个样本容量N分别为100，400，1000的时间序列：
（1）模型1，三次方模型：DGP为：
，这里wt为一随机游走序列，满足初始值为w0＝0，u1t与u2t为两独立的高斯白噪声序列。
（2）模型2，平方模型：DGP为：
，这里wt为一随机游走序列，满足初始值为w0＝0，u1t与u2t为两独立的高斯白噪声序列。
（3）模型3，二次多项式模型：DGP为：
，这里wt为一随机游走序列，满足初始值为w0＝0，u1t与u2t为两独立的高斯白噪声序列。
这里，以改进的BP-LM算法为例，其对上述三种非线性模型的估计效果如图7-9所示。
由图7-9可见，当非平稳时间序列间确实存在非线性结构时，神经网络模型能够很好地析出数据样本间的非线性函数关系。
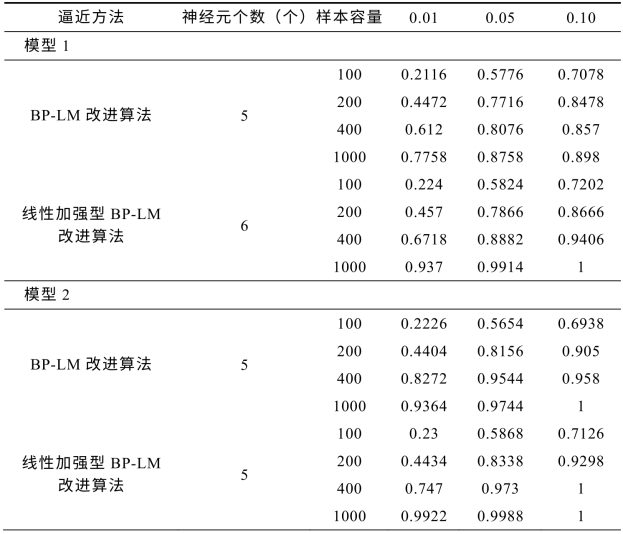
进一步，分别对上述三种模型的DGP序列重复5000次，对应用改进的BP-LM算法神经网络逼近后的残差序列进行ADF检验，考察其功效，结果如表7-3所示。
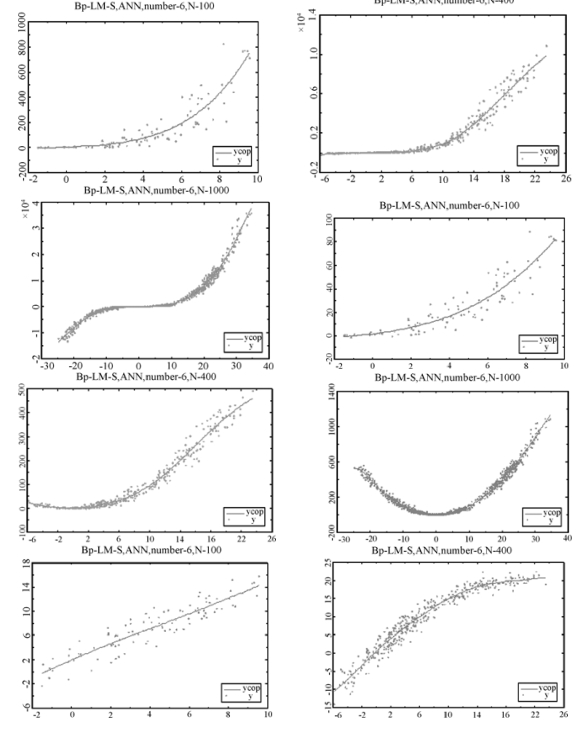
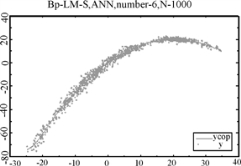
图7-9 图中第1、2、3排从左至右，分别对应模型（1）、（2）、（3）在样本容量分别为100，400，1000的情形
表7-3 改进的BP-LM算法神经网络的各模型非线性协整检验功效
续表
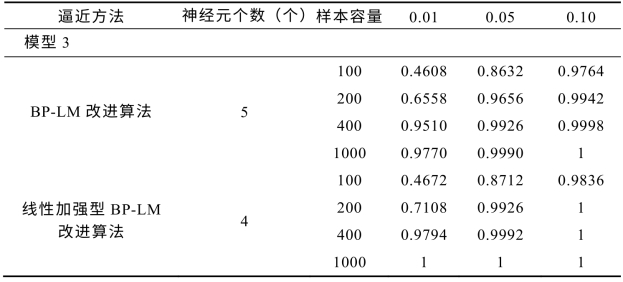
由表7-3可知，对于三种模型形式，两种算法均表现出良好的功效并随样本容量的增大而趋向100%，线性加强型BP-LM改进算法要优于BP-LM改进算法。