画“箭头”的特殊句式
4.1三种性质判断

以上3个句式,都不是假言判断,句式①是性质判断中的单称判断,句式②是性质判断中的特称判断,句式③是性质判断中的全称判断(性质判断的相关知识见本书第2章第3节)。
但是,在很多题目中,如果我们用“→”把这些句式表示出来,就会使做题变得简单、快速、准确。因此,可以把上述3个例句符号化为:
句式①:冬雨→女神。
句式②:有的明星→女神。
句式③:明星→女神。
其中箭头可读作“是”,且句式③中的“所有的”可省略。
需要注意的是,虽然我们用箭头表示了这三个判断,但并不表示这三个判断是假言判断,也不代表这三个判断和句式①、②、③完全等价。我们这样做的目的仅仅是为了快速做题、快速得分、考上研究生。
4.2 A必须B
先看下面的例子:
想要考上研究生,必须努力学习。
【分析】
很多同学对这个例子会有疑问,因为“必须”这两个字显然是在表达“必要”的意思,然后再根据口诀“必要条件后推前”,得到“努力学习→考上研究生”。但其实这样是错误的。
“想要考上研究生,必须努力学习”的意思是:“如果想要考上研究生,那么努力学习是必要的”,也就是说,“如果想要考上研究生,那么一定要努力”,即“考上研究生”是“努力学习”的充分条件。反之,“努力学习”是“考上研究生”的必要条件,只有努力学习才能考上研究生,不努力学习肯定考不上研究生。可见,“必须”确实在表达“必要”的含义,但是,这种“必要性”要看谁相对于谁来说。
即:
想要考上研究生,必须努力学习。
等价于:如果想要考上研究生,那么必须努力学习。
等价于:只有努力学习,才能考上研究生。
等价于:不努力学习,考不上研究生。
综上,如图2-5所示:
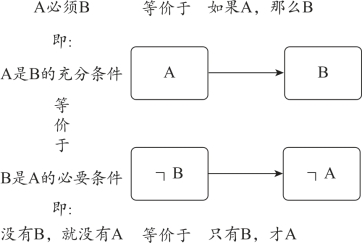
图2-5
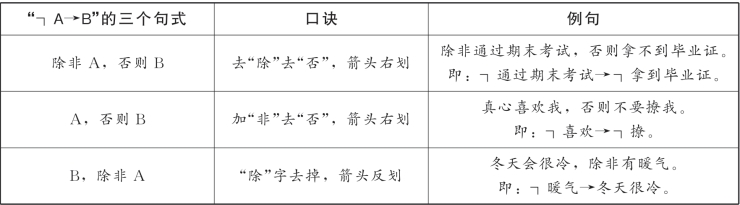
4.3“┐A→B”的三种句式
“┐A→B”,读作“非A推B”,有三种表达方式:“除非A,否则B”“A,否则B”“B,除非A”。
(1)除非A,否则B。
例如:
除非你买房,否则我不嫁你。
这句话的意思是,买房是我嫁给你的必要条件,你必须得买房,如果你不买房,我就不嫁给你,即:┐买房→不嫁。
【口诀6】去“除”去“否”,箭头右划
(2)A,否则B。
例如:
你买房,否则我不嫁你。
这句话的意思与“除非你买房,否则我不嫁你”相同,还是在强调买房的必要性。你得买房,如果你不买房,我就不嫁给你,即:┐买房→不嫁。
【口诀7】加“非”去“否”,箭头右划
(3)B,除非A。
例如:
我不嫁你,除非你买房。
这句话的意思与“除非你买房,否则我不嫁你”相同,即:┐买房→不嫁。
【口诀8】“除”字去掉,箭头反划
综上,可得表2-3:
表2-3
【一个例外】
若想人不知,除非己莫为。
这句话的意思是:如果你不想让别人知道,那么你不要去做,即:不想让别人知道→不要做。因此,这句话不能用上述口诀。
典型例题
例5 只有认识错误,才能改正错误。
以下各项都准确地表达了上述断定的含义,除了:
A.除非认识错误,否则不能改正错误。
B.如果不认识错误,那么不能改正错误。
C.如果改正错误,说明已经认识了错误。
D.只要认识错误,就一定能改正错误。
E.不能改正错误,除非认识错误。
【解析】题干:根据必要条件后推前,认识←改正=┐认识→┐改正。
A项,去“除”去“否”,箭头右划,得:┐认识→┐改正,与原判断等价。
B项,充分条件前推后,得:┐认识→┐改正,与原判断等价。
C项,充分条件前推后,得:改正→认识,与原判断等价。
D项,充分条件前推后,得:认识→改正,根据“箭头指向原则”可知,与原判断不等价。
E项,“除”字去掉,箭头反划,得:┐认识→┐改正,与原判断等价。
【答案】D
