性质判断的负判断
3.1性质判断的负判断的原理
(1)“并非所有”等价于“有的不”
矛盾关系必为一真一假,因此,在性质判断对当关系图(六边形)中,我们否定了左上角的“所有”,相当于肯定了右下角的矛盾命题“有的不”,如图2-22所示:
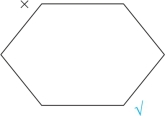
图2-22
例①:
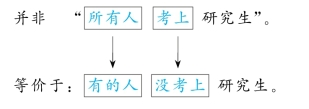
(2)“并非所有不”等价于“有的”
矛盾关系必为一真一假,因此,在性质判断对当关系图(六边形)中,我们否定了右上角的“所有不”,相当于肯定了左下角的矛盾命题“有的”,如图2-23所示:
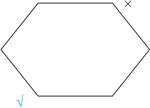
图2-23
例②:
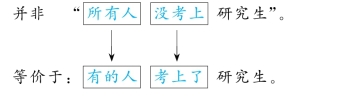
(3)“并非有的”等价于“所有不”
矛盾关系必为一真一假,因此,在性质判断对当关系图(六边形)中,我们否定了左下角的“有的”,相当于肯定了右上角的矛盾命题“所有不”,如图2-24所示:
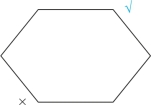
图2-24
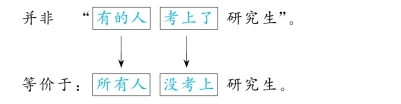
例③:
(4)“并非有的不”等价于“所有”
矛盾关系必为一真一假,因此,在性质判断对当关系图(六边形)中,我们否定了右下角的“有的不”,相当于肯定了左上角的矛盾命题“所有”,如图2-25所示:
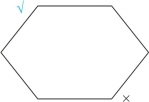
图2-25
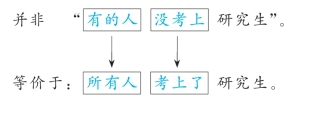
例④:
3.2性质判断的负判断的替换法口诀
观察例①、②、③、④可知,四个例子都有以下规律:
“并非”+“性质判断”,等价于去掉前面的“并非”,再将原“性质判断”进行如下变化:
【口诀14】
肯定变否定,否定变肯定;
所有变有的,有的变所有。
【易错点】
①性质判断前面加“并非”或者其他否定词以后,做口诀14中的变化会出现这个“并非+性质判断”的等价判断。如果性质判断前面没有“并非”或者其他否定词,直接用口诀14就会变成原性质判断的矛盾命题。
②口诀14中的“肯定”“否定”指的是谓语动词。定语部分的肯定、否定不能变化。
例如:
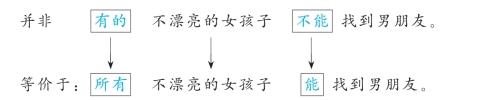
本例中的判断对象“不漂亮的女孩子”是不能变化的,如果变成了“漂亮的女孩子”就偷换了论证对象。
③涉及负判断的题目,还有一些其他特殊的使用技巧,老吕将在本书的“母题篇”中给大家讲解。
典型例题
例22 写出下列判断的等价判断。
(1)并非所有地铁都在地下开。
(2)并非所有地铁都不在地下开。
(3)并非有的地铁在地下开。
(4)并非有的地铁不在地下开。
【解析】
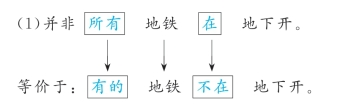
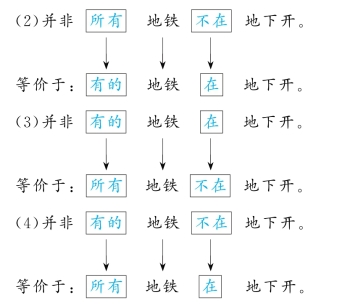
例23 写出下列判断的等价判断。
(1)鸟不都会飞。
(2)并非鸟不都会飞。
(3)并非鸟都会飞。
(4)并非鸟都不会飞。
【解析】
“都”的含义
①当“所有”和“都”连用时,“都”其实是个语气助词。
如:所有鸟都会飞。把这个“都”去掉以后,不影响原意。
②当“都”被独立使用时,“都”等价于“所有”。
如:“鸟都会飞”等价于“所有鸟会飞”。
(1)“都”=“所有”,“不都”=“不是所有”=“有的不”。
故原判断等价于:不是所有鸟都会飞=有的鸟不会飞。
(2)“不都”=“不是所有”,“并非不都”=“并非不是所有”=“所有”(双重否定表示肯定)。
故原判断等价于:所有鸟会飞。
(3)“都”=“所有”,“并非都”=“并非所有”=“有的不”。
故原判断等价于:不是所有鸟都会飞=有的鸟不会飞。
(4)“都”=“所有”,“并非都不”=“并非所有不”=“有的”。
故原判断等价于:并非所有鸟不会飞=有的鸟会飞。
