模态判断的对当关系
与性质判断一样,模态判断之间的关系也可以分为四类:矛盾关系、反对关系、下反对关系、推理关系,如图2-26所示:
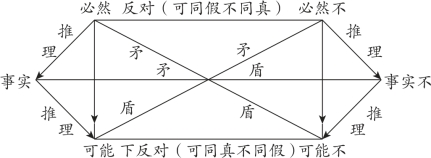
图2-26
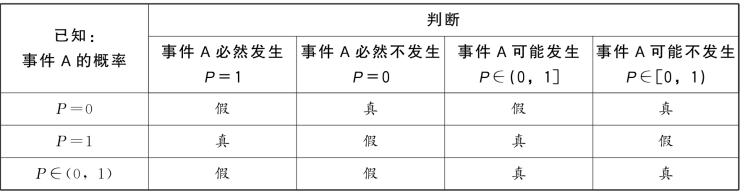
我们知道,一个事件发生的可能性只有三种:必然发生(即概率P=1),必然不发生(即概率P=0),可能发生也可能不发生[即概率P∈(0,1)]。这样,可得表2-14:
表2-14
2.1矛盾关系
在表2-14中,“必然”和“可能不”这两列,永远为一真一假。“必然不”和“可能”这两列,永远为一真一假。
这种永远一真一假的关系,称为矛盾关系。故“必然”和“可能不”矛盾;“必然不”和“可能”矛盾。
集合视角看矛盾关系
从集合的角度来看,矛盾的两个集合没有交集而且加起来是全集。
“事件A必然发生P=1”和“事件A可能不发生P∈[0,1)”没有交集而且加起来是全集[0,1],故二者是矛盾关系。
同理,“事件A必然不发生P=0”和“事件A可能发生P∈(0,1]”没有交集而且加起来是全集[0,1],故二者也是矛盾关系。
当然,“事实上事件A发生”和“事实上事件A不发生”显然是矛盾的。故“事实”和“事实不”矛盾。
总之,位于模态判断对当关系图(即图2-26)中对角线上的判断是矛盾关系,二者必有一真一假,有如下三组:
“必然”与“可能不”;
“必然不”与“可能”;
“事实”与“事实不”。
2.2反对关系
观察表2-14中“必然”和“必然不”这两列。可知:
当“P=0”时,“必然”为假、“必然不”为真。
当“P=1”时,“必然”为真、“必然不”为假。
当“P∈(0,1)”时,“必然”和“必然不”均为假。
即,“必然”和“必然不”的真假情况可能是一真一假,也可能是两假,即二者至少一假。我们把这种关系称为反对关系。
总之,“必然”和“必然不”是反对关系,二者至少有一假。已知一个为真,另外一个必为假;已知一个为假,另外一个可能为真也可能为假。
【口诀15】两个必然,至少一假;一真另必假,一假另不定
2.3下反对关系
观察表2-14中“可能”和“可能不”这两列。可知:
当“P=0”时,“可能”为假、“可能不”为真。
当“P=1”时,“可能”为真、“可能不”为假。
当“P∈(0,1)”时,“可能”和“可能不”均为真。
即,“可能”和“可能不”的真假情况可能是一真一假,也可能是两真,即二者至少一真。我们把这种关系称为下反对关系。
总之,“可能”和“可能不”是下反对关系,二者至少有一真。已知一个为假,另外一个必为真;已知一个为真,另外一个可能为真也可能为假。
【口诀16】两个可能,至少一真;一假另必真,一真另不定
2.4推理关系
(1)必然→事实→可能
观察模态判断对当关系图(即图2-26六边形)的左侧,自上到下显然有如下推理关系(也叫从属关系),如图2-27所示:

图2-27
①此处满足“箭头指向原则”,即:有箭头指向则为真,没有箭头指向则可真可假。
如:已知“事件A可能发生”为真,那么事件A发生了吗?不知道。事件A必然发生吗?也不知道。
②此处满足“逆否原则”,即“可能”为假→“事实”为假→“必然”为假,如图2-28所示:
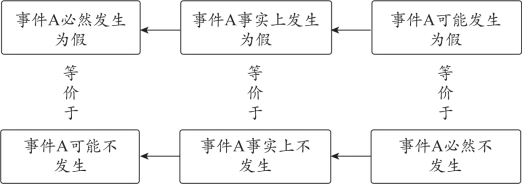
图2-28
(2)必然不→事实不→可能不
观察模态判断对当关系图(即图2-26六边形)的右侧,自上到下显然有如下推理关系,如图2-29所示:

图2-29
①此处满足“箭头指向原则”,即:有箭头指向则为真,没有箭头指向则可真可假。
如:已知“事件A可能不发生”为真,那么事件A没发生吗?不知道。事件A必然不发生吗?也不知道。
②此处满足“逆否原则”,即“可能不”为假→“事实不”为假→“必然不”为假,如图2-30所示:
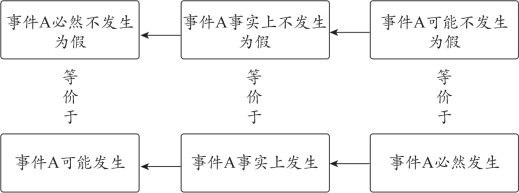
图2-30
综上所述,在模态判断对当关系图(即图2-26六边形)中,无论是左侧还是右侧的推理关系都存在以下口诀:
【口诀17】上真下必真,下假上必假;反之则不定
说明:“反之则不定”的意思是“下真上不定,上假下不定”。
综上所述,模态判断和性质判断的对当关系原理完全相同,解题方法也完全相同。
典型例题
例24 已知“他必然会拿冠军”为真,则以下判断哪些必然为真,哪些必然为假,哪些可真可假?
(1)他必然不会拿冠军。
(2)他可能会拿冠军。
(3)他可能不会拿冠军。
(4)事实上,他会拿冠军。
(5)事实上,他不会拿冠军。
【解析】
(1)项,根据口诀“两个必然,至少一假;一真另必假,一假另不定”,已知“他必然会拿冠军”为真,则“他必然不会拿冠军”为假。
(2)项,根据“必然→事实→可能”,可知“必然→可能”,故此项为真。
(3)项,“必然”与“可能不”矛盾,根据矛盾关系,二者必有一真一假,已知“他必然会拿冠军”为真,则“他可能不会拿冠军”为假。
(4)项,根据“必然→事实→可能”,可知“必然→事实”,故此项为真。
(5)项,“事实”与“事实不”矛盾,根据矛盾关系,二者必有一真一假,已知(4)项“事实上,他会拿冠军”为真,则“事实上,他不会拿冠军”为假。
【秒杀技巧】画一个六边形,代表模态判断对当关系图,已知“他必然会拿冠军”为真,即左上角为真,画“√”(我们用黑色表示已知条件),如图2-31所示:
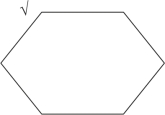
图2-31
根据口诀“上真下必真”,可知六边形的左侧均为真,画“√”;对角线为矛盾命题,故六边形的右侧均为假,画“×”(我们用蓝色表示推理出来的情况),如图2-32所示:
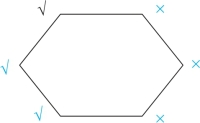
图2-32
即可迅速判断(1)项为假,(2)项为真,(3)项为假,(4)项为真,(5)项为假。
例25 已知“豆豆可能是网红”为假,则以下判断哪些必然为真,哪些必然为假,哪些可真可假?
(1)豆豆必然是网红。
(2)豆豆必然不是网红。
(3)豆豆可能不是网红。
(4)豆豆是网红。
(5)豆豆不是网红。
【解析】
(1)项,根据“‘可能’为假→‘事实’为假→‘必然’为假”,可知“可能”为假→“必然”为假,已知“豆豆可能是网红”为假,则“豆豆必然是网红”为假,即此项为假。
(2)项,“可能”与“必然不”矛盾,根据矛盾关系,二者必有一真一假,已知“豆豆可能是网红”为假,则“豆豆必然不是网红”为真,即此项为真。
(3)项,根据“必然不→事实不→可能不”,结合(2)项,可知此项为真。
(4)项、(5)项,根据“必然不→事实不→可能不”,结合(2)项,可知(4)项为假,(5)项为真。
【秒杀技巧】画一个六边形,代表模态判断对当关系图,已知“豆豆可能是网红”为假,即左下角为假,画“×”(我们用黑色表示已知条件),如图2-33所示:
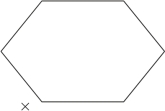
图2-33
根据口诀“下假上必假”,可知六边形的左侧均为假,画“×”;对角线为矛盾命题,故六边形的右侧均为真,画“√”(我们用蓝色表示推理出来的情况),如图2-34所示:
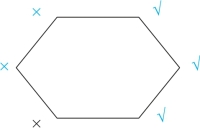
图2-34
即可迅速判断(1)项为假,(2)项为真,(3)项为真,(4)项为假,(5)项为真。
