性质判断的对当关系
性质判断之间的关系可以分为四类:矛盾关系、反对关系、下反对关系、推理关系,如图2-8所示:
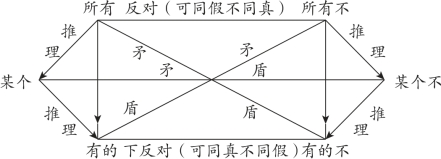
图2-8
下面,我们用一个例子来说明上图。假定我们班共有10人,对于我们班的同学的考研情况,有以下6个判断,如表2-11所示:
表2-11
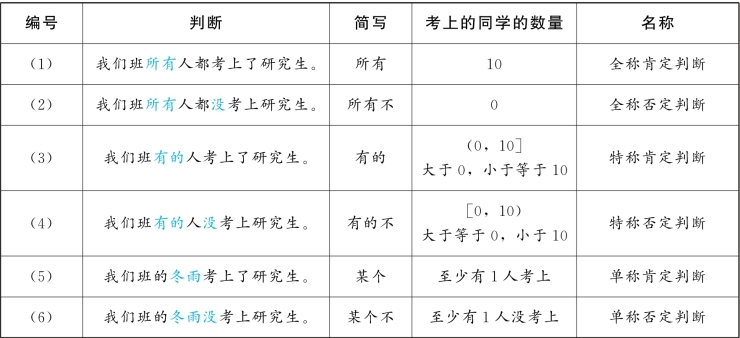
我们把我们班考上研究生的同学的数量关系分为三类:全部都考上(10人考上)、全部没考上(0人考上)、一部分考上一部分没考上(1到9人考上),可知这三类囊括了我们班同学考上研究
生的所有可能情况。即可得表2-12:
表2-12
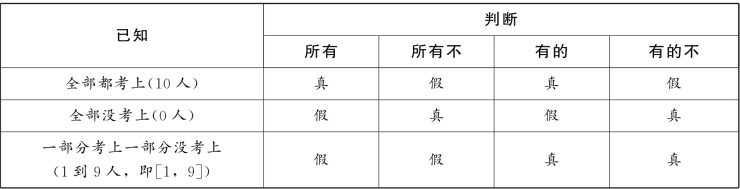
观察表2-12,可得以下四种关系。
2.1矛盾关系
在表2-12中,“所有”和“有的不”这两列,永远为一真一假。“所有不”和“有的”这两列,永远为一真一假。
这种永远一真一假的关系,称为矛盾关系。故“所有”和“有的不”矛盾;“有的”和“所有不”矛盾。
当然,“冬雨考上了研究生”和“冬雨没考上研究生”显然是矛盾的。故“某个”和“某个不”矛盾。
总之,位于性质判断对当关系图(即图2-8)中对角线上的判断是矛盾关系,二者必有一真一假,有如下三组:
“所有”与“有的不”;
“所有不”与“有的”;
“某个”与“某个不”。
【易错点】
①上述三组关系中的“所有”其实不是单纯的“所有”,后面应该是有主语和谓语的,比如“所有母鸡(主语)下蛋了(谓语)”;同理,“所有不”也不是单纯的“所有不”,后面应该是有主语和谓语的,只是为了快速做题,我们将后面的主谓部分省略了而已。其中“不”指的是谓语动词的否定。比如“所有母鸡(主语)没下蛋(否定的谓语)”。
同理,“有的”和“有的不”指的也是“有的A(主语)怎么样(谓语)”和“有的A(主语)没怎么样(否定的谓语)”。
②上述三组关系中的“某个”指的是一个具体的对象(theone),而不是不确定的一个(someone)。
③矛盾命题总是一真一假,故若有矛盾命题A和B,已知A为真,则B必为假;已知A为假,则B必为真;反之亦然。当然,如果我们无法判断A的真假(即A可能为真也可能为假),那么也就无法判断它的矛盾命题B的真假(即B可能为假也可能为真)。
2.2反对关系
观察表2-12中“所有”和“所有不”这两列。可知:
当“全部都考上(10人)”时,“所有”为真、“所有不”为假。
当“全部没考上(0人)”时,“所有”为假、“所有不”为真。
当“一部分考上一部分没考上(1到9人)”时,“所有”和“所有不”均为假。
即,“所有”和“所有不”的真假情况可能是一真一假,也可能是两假,即二者至少一假。我们把这种关系称为反对关系。
总之,“所有”和“所有不”是反对关系,二者至少有一假。已知一个为真,另外一个必为假;已知一个为假,另外一个可能为真也可能为假。
【口诀11】两个所有,至少一假;一真另必假,一假另不定
2.3下反对关系
观察表2-12中“有的”和“有的不”这两列。可知:
当“全部都考上(10人)”时,“有的”为真、“有的不”为假。
当“全部没考上(0人)”时,“有的”为假、“有的不”为真。
当“一部分考上一部分没考上(1到9人)”时,“有的”和“有的不”均为真。
即,“有的”和“有的不”的真假情况可能是一真一假,也可能是两真,即二者至少一真。我们把这种关系称为下反对关系。
总之,“有的”和“有的不”是下反对关系,二者至少有一真。已知一个为假,另外一个必为真;已知一个为真,另外一个可能为真也可能为假。
【口诀12】两个有的,至少一真;一假另必真,一真另不定
2.4推理关系
(1)所有→某个→有的
观察性质判断对当关系图(即图2-8六边形)的左侧,自上到下显然有如下推理关系(也叫从属关系),如图2-9所示:

图2-9
①此处满足“箭头指向原则”,即:有箭头指向则为真,没有箭头指向则可真可假。
如:已知“有的人考上了研究生”为真,那么,这个考上研究生的人是冬雨吗?不知道。是所有人考上了研究生吗?也不知道。
②此处满足“逆否原则”,即“有的”为假→“某个”为假→“所有”为假,如图2-10所示:
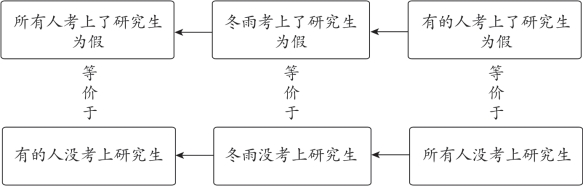
图2-10
(2)所有不→某个不→有的不
观察性质判断对当关系图(即图2-8六边形)的右侧,自上到下显然有如下推理关系,如图2-11所示:

图2-11
①此处满足“箭头指向原则”,即:有箭头指向则为真,没有箭头指向则可真可假。
如:已知“有的人没考上研究生”为真,那么,这个没考上研究生的人是冬雨吗?不知道。是所有人都没考上研究生吗?也不知道。
②此处满足“逆否原则”,即“有的不”为假→“某个不”为假→“所有不”为假,如图2-12所示:
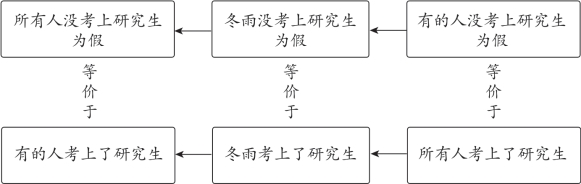
图2-12
综上所述,在性质判断对当关系图(即图2-8六边形)中,无论是左侧还是右侧的推理关系都存在以下口诀:
【口诀13】上真下必真,下假上必假;反之则不定
说明:“反之则不定”的意思是“下真上不定,上假下不定”。
典型例题
例19 已知“所有女明星颜值很高”为真,则以下判断哪些必然为真,哪些必然为假,哪些可真可假?
(1)有的女明星颜值不高。
(2)有的女明星颜值高。
(3)所有女明星颜值不高。
(4)女明星baby颜值不高。
(5)女明星冬雨颜值高。
【解析】根据矛盾关系可知,“所有”与“有的不”矛盾,故(1)项必为假。
根据“所有→某个→有的”可知,(5)、(2)项必为真。
根据反对关系口诀“两个所有,至少一假;一真另必假,一假另不定”,故(3)项必为假。
根据矛盾关系可知,“某个”和“某个不”矛盾,又知(5)项为真,故(4)项必为假。
【秒杀技巧】画一个六边形,代表性质判断对当关系图,已知“所有女明星颜值很高”为真,即左上角为真,画“√”(我们用黑色表示已知条件),如图2-13所示:
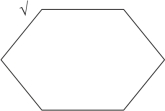
图2-13
根据口诀“上真下必真”,可知六边形的左侧均为真,画“√”(我们用蓝色表示推理出来的情况),如图2-14所示:
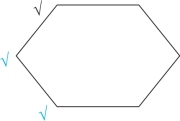
图2-14
对角线为矛盾命题,故六边形的右侧均为假,画“×”(我们用蓝色表示推理出来的情况),如图2-15所示:
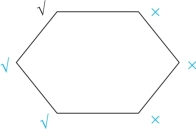
图2-15
即可迅速判断(1)项为假,(2)项为真,(3)项为假,(4)项为假,(5)项为真。
例20 已知“有些留学生来自韩国”为真,则以下哪个判断必然为假?
A.有些留学生不是来自韩国。
B.所有留学生来自韩国。
C.所有留学生都不是来自韩国。
D.秀智是留学生,来自韩国。
E.仲基是留学生,但不是来自韩国。
【解析】
A项,根据下反对关系口诀“两个有的,至少一真;一假另必真,一真另不定”,可知此项可真可假。
B项,根据“所有→某个→有的”和“箭头指向原则”可知,“有的”不能推“所有”,故此项可真可假。
C项,根据“有的”和“所有不”是矛盾关系,二者必有一真一假,已知“有的”为真,故“所有不”为假,即此项必为假。
D项,根据“所有→某个→有的”和“箭头指向原则”可知,“有的”不能推“某个”,故此项可真可假。
E项,根据矛盾关系可知,“某个”和“某个不”矛盾,已知“某个”可真可假,故此项可真可假。
【秒杀技巧】画一个六边形,代表性质判断对当关系图,已知“有些留学生来自韩国”为真,即左下角为真,画“√”(我们用黑色表示已知条件),如图2-16所示:
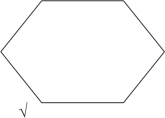
图2-16
对角线为矛盾命题,故六边形的右上角为假,画“×”(我们用蓝色表示推理出来的情况),如图2-17所示:
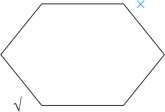
图2-17
根据口诀“下真上不定”,可知六边形左上和左中均为可真可假,其对角线也为可真可假,画“?”(我们用蓝色表示推理出来的情况),如图2-18所示:
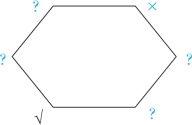
图2-18
即可迅速判断A项可真可假,B项可真可假,C项为假,D项可真可假,E项可真可假。
【答案】C
例21 培光街道发现有保姆未办暂住证。
如果上述断定为真,则以下哪项不能确定真假?
Ⅰ.培光街道所有保姆都未办暂住证。
Ⅱ.培光街道所有保姆都办了暂住证。
Ⅲ.培光街道有保姆办了暂住证。
Ⅳ.培光街道的保姆陈秀英办了暂住证。
A.Ⅰ、Ⅱ、Ⅲ、Ⅳ。 B.仅Ⅰ、Ⅲ和Ⅳ。 C.仅Ⅰ。
D.仅Ⅰ和Ⅳ。 E.仅Ⅳ。
【解析】根据“所有不→某个不→有的不”和“箭头指向原则”可知,“有的不”为真,则“所有不”真假不定,故I项可真可假。
“有的不”和“所有”是矛盾关系,二者必有一真一假,已知“有的不”为真,故“所有”为假,即Ⅱ项必为假。
根据下反对关系口诀“两个有的,至少一真;一假另必真,一真另不定”,已知“有的不”为真,故“有的”真假不定,即Ⅲ项可真可假。
从题干无法知道陈秀英有没有办暂住证,故Ⅳ项可真可假。
【秒杀技巧】画一个六边形,代表性质判断对当关系图,已知“有的保姆未办暂住证”为真,即右下角为真,画“√”(我们用黑色表示已知条件),如图2-19所示:
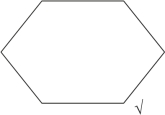
图2-19
对角线为矛盾命题,故六边形的左上角为假,画“×”(我们用蓝色表示推理出来的情况),如图2-20所示:
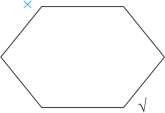
图2-20
根据口诀“下真上不定”,可知六边形的右上和右中均为可真可假,其对角线也为可真可假,画“?”(我们用蓝色表示推理出来的情况),如图2-21所示:
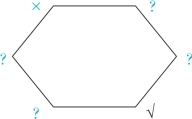
图2-21
即可迅速判断Ⅰ项可真可假,Ⅱ项为假,Ⅲ项可真可假,Ⅳ项可真可假。
综上,B项正确。
【答案】B
