模态判断的概念与数学意义

1.模态判断的概念与数学意义

1.1模态判断的概念

模态判断又称模态命题,用来陈述事件发生的必然性和可能性。一般用“必然”“可能”“必然不”“可能不”这四个“模态词”来表示模态判断。

例如:

冬雨必然爱老吕。

杀手必然不会藏匿于此处。

嫌疑人可能具备作案动机。

你可能不是一个凡人。

1.2模态判断的数学意义

如果我们用概率来表达模态判断,那么可得表2-13:

表2-13

由表2-13可知,“可能”和“可能不”含义不同:

一个事件必然发生(P＝1),那么它“可能发生”是真的;一个事件必然不发生(P＝0),那么它“可能发生”是假的,因此,可能事件的概率为P∈(0,1],为左开右闭区间。

一个事件必然发生(P＝1),那么它“可能不发生”是假的;一个事件必然不发生(P＝0),那么它“可能不发生”是真的,因此,可能不事件的概率为P∈[0,1),为左闭右开区间。

1.3易错点:“必然”和“事实”等价吗?

“事件A必然发生”和“事件A事实发生”并不等价。

“事件A必然发生”的意思是事件A发生的概率为百分之百,但这并不代表事件A已经发生了。比如,“张三必然会死”这句话为真,并不代表“张三事实上死了”。

那么,一件事发生了,这件事发生的概率是1(必然)吗?也不对。因为“可能事件”也是有可能发生成为事实的。比如,我扔一枚硬币出现了正面,并不代表扔一枚硬币出现正面的概率是1。通过数学知识我们知道,“扔一枚硬币出现正面”是一个概率为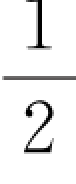的可能事件,只不过这一次刚好出现了正面而已。