假言判断的负判断
负判断,即矛盾命题。那么假言判断的矛盾命题是什么呢?
4.1充分条件的负判断
先看一个例子:
你男朋友对你承诺:等你毕业了,我一定娶你。
在什么情况下,你男朋友对你的承诺没有做到呢?显然是“你毕业了,但是他没娶你”,这个“大猪蹄子”说话不算话。
可见,“毕业了→娶你”与“毕业了∧┐娶你”矛盾。
通俗地说,充分条件A→B的含义是“有它就行”,与之矛盾的判断就是“有它,但是不行”,即“A∧┐B”。
综上:
充分条件“A→B”的矛盾命题是“A∧┐B”。
可见,“并非(A→B)”与“A∧┐B”等价,可得公式:
┐(A→B)=A∧┐B。
【证明】如图2-6所示。
典型例题
例16 小张承诺:如果天不下雨,我一定去听音乐会。
以下哪项如果为真,说明小张没有兑现承诺?
Ⅰ.天没下雨,小张没去听音乐会。
Ⅱ.天下雨,小张去听了音乐会。
Ⅲ.天下雨,小张没去听音乐会。
A.仅Ⅰ。 B.仅Ⅱ。 C.仅Ⅲ。
D.仅Ⅰ和Ⅱ。 E.Ⅰ、Ⅱ和Ⅲ。
【解析】小张承诺:┐下雨→听音乐会。
没有兑现承诺,即:┐(┐下雨→听音乐会)=┐下雨∧┐听音乐会,故Ⅰ项正确。
小张的承诺等价于:┐听音乐会→下雨。根据箭头指向原则,“下雨”后面没箭头,可见,如果下雨了,小张可以去听音乐会也可以不去听音乐会,故Ⅱ项和Ⅲ项并不违背小张的承诺。
【答案】A
4.2必要条件的负判断
先看一个例子:
不报老吕的班,一定考不上研究生。
在什么情况下,这句话为假呢?显然是“没报老吕的班,但是考上了研究生”。
可见:“不报老吕的班→考不上研究生”与“不报老吕的班∧考上了研究生”矛盾。
通俗地说,必要条件的含义是“没它不行”,与之矛盾的判断就是“没它也行”,即“┐A∧B”。
综上:
必要条件“┐A→┐B”的矛盾命题为“┐A∧B”。
可见,“并非(┐A→┐B)”与“┐A∧B”等价,可得公式:
┐(┐A→┐B)=┐A∧B。
【证明】如图2-7所示。
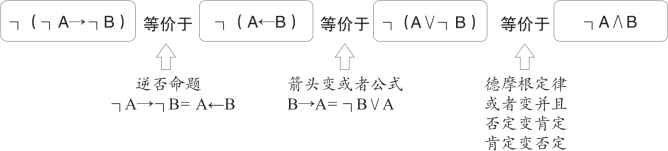
图2-7
根据逆否原则“┐A→┐B”等价于“B→A”,而“┐A∧B”又等价于“B∧┐A”。
可见公式:┐(┐A→┐B)=┐A∧B。
可以写成:┐(B→A)=B∧┐A,即肯定了箭头前面的(前件),否定了箭头指向的(后件)。
再观察充分条件的负判断公式:┐(A→B)=A∧┐B,也是肯定了箭头前面的(前件),否定了箭头指向的(后件)。
可见,不论是充分条件的矛盾命题还是必要条件的矛盾命题,都可以用以下口诀来记忆。
【口诀10】箭头的矛盾命题为:肯前且否后
典型例题
例17 王颖:“感情是婚姻的基础。”
李剑:“我不同意。”
李剑的意思是:
A.结婚,但没有感情。 B.没结婚,也没有感情。
C.没结婚,但有感情。 D.如果有感情,就应该结婚。
E.李剑不结婚。
【解析】王颖:感情是婚姻的基础=只有有感情,才会有婚姻,符号化为:婚姻→感情。
李剑:┐(婚姻→感情)=婚姻∧┐感情。所以,李剑的意思是结婚,但没有感情。
故A项正确。
【答案】A
4.3充分必要条件的负判断
根据前面所学知识,充分必要条件“A↔B”,本质上来讲是个等价关系,A和B或者都发生,或者都不发生。它与发生且仅发生一个正好矛盾,即:
①A↔B与A∀B矛盾。
②┐(A↔B)=(A∧┐B)∀(┐A∧B)。
【注意】
以上公式②也可以写成┐(A↔B)=(A∧┐B)∨(┐A∧B)。这是因为,“A∧┐B”与“┐A∧B”不可能同时为真,此时用“∨”表示和用“∀”表示的含义是等同的。
典型例题
例18 张珊说:“当且仅当天下雨,地上才会湿。”
以下哪项如果为真,说明张珊的话为假?
Ⅰ.天下雨了,地上湿了。
Ⅱ.天下雨了,地上没湿。
Ⅲ.天没下雨,地上湿了。
A.仅Ⅰ。 B.仅Ⅱ。 C.仅Ⅲ。
D.仅Ⅱ和Ⅲ。 E.Ⅰ、Ⅱ和Ⅲ。
【解析】张珊:天下雨↔地上湿。
张珊的话为假,即┐(天下雨↔地上湿),等价于:(天下雨∧┐地上湿)∨(┐天下雨∧地上湿)。
故,如果出现“天下雨∧┐地上湿”或者“┐天下雨∧地上湿”,都可以说明张珊的话为假,故Ⅱ项和Ⅲ项均正确。
【答案】D
