5:五种条件定式
关系推理题常与演绎推理题联合考查,由于这类题的解题基础是演绎推理,尤其常以串联推理和二难推理为基础,因此,我们称这类题为综合演绎推理,并归类到演绎推理中。定式1“肯前否后式”、定式2“二难推理式”其实考的都是演绎推理的知识。在本节中,我们将综合演绎推理和关系推理一起进行总结。
定式1肯前否后式
若在关系推理题或综合演绎推理题中,已知条件或选项中出现假言判断,则:
(1)若能确定已知条件中假言判断的前件为真,则可继续向后推出新的事实。如前面内容中的例23。
(2)若能确定已知条件中假言判断的后件为假,则可通过逆否推出新的事实。如前面内容中的例24、后面内容中的例34。
(3)若选项中出现新的假言判断,则选项中假言判断的前件可作为已知条件使用;或者否定其后件作为已知条件使用。如后面内容中的例35。
典型例题
例34 下面两题基于以下题干:
江海大学的校园美食节开幕了,某女生宿舍有5人积极报名参加此次活动,她们的姓名分别为金粲、木心、水仙、火珊、土润。举办方要求,每位报名者只做一道菜品参加评比,但需自备食材。限于条件,该宿舍所备食材仅有5种:金针菇、木耳、水蜜桃、火腿和土豆,要求每种食材只能有2人选用,每人又只能选用2种食材,并且每人所选食材名称的第一个字与自己的姓氏均不相同。已知:
①如果金粲选水蜜桃,则水仙不选金针菇。
②如果木心选金针菇或土豆,则她也须选木耳。
③如果火珊选水蜜桃,则她也须选木耳和土豆。
④如果木心选火腿,则火珊不选金针菇。
(1)根据上述信息,可以得出以下哪项?
A.木心选用水蜜桃、土豆。 B.水仙选用金针菇、火腿。
C.土润选用金针菇、水蜜桃。 D.火珊选用木耳、水蜜桃。
E.金粲选用木耳、土豆。
(2)如果水仙选用土豆,则可以得出以下哪项?
A.木心选用金针菇、水蜜桃。 B.金粲选用木耳、火腿。
C.火珊选用金针菇、土豆。 D.水仙选用木耳、土豆。
E.土润选用水蜜桃、火腿。
【解析】将题干信息形式化:
①金粲选水蜜桃→┐水仙选金针菇。
②木心:金针菇∨土豆→木耳。
③火珊:水蜜桃→木耳∧土豆。
④木心选火腿→┐火珊选金针菇。
第(1)题:
题干给出的条件几乎都是假言判断,要想推出新的事实,常常考虑肯定假言判断的前件,或否定假言判断的后件。
突破口1:否定后件式。
由“每人所选食材名称的第一个字与自己的姓氏均不相同”可知,木心不能选木耳,即否定了题干信息②的后件,故由②逆否可得,木心:┐木耳→┐金针菇∧┐土豆。又由“每人只能选用2种食材”可知,木心:火腿∧水蜜桃。
由题干信息④可知,木心选火腿→┐火珊选金针菇。
突破口2:假设归谬法(找矛盾)。
由题干信息③可得,若火珊选水蜜桃,则她也必须选木耳和土豆,与题干信息“每人只能选用2种食材”矛盾,故火珊不能选水蜜桃。
由于此题涉及两组元素的匹配,可使用表格法。根据上述分析,可得表3-9:
表3-9
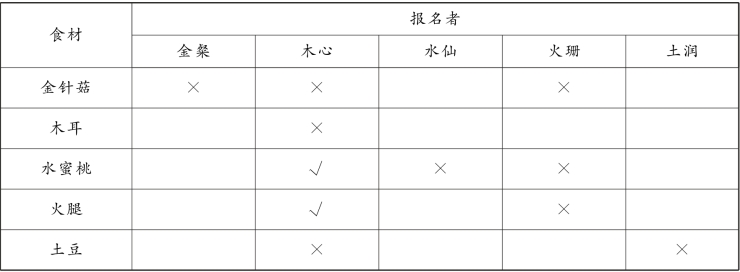
根据题干信息“要求每种食材只能有2人选用,每人又只能选用2种食材”可得,木心:火腿∧水蜜桃;火珊:木耳∧土豆;水仙选金针菇∧土润选金针菇。
由题干信息①可知,金粲选水蜜桃→┐水仙选金针菇=水仙选金针菇→金粲不选水蜜桃,可得表3-10:
表3-10
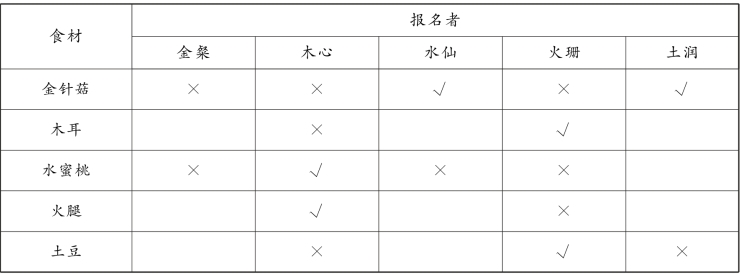
根据题干信息“要求每种食材只能有2人选用,每人又只能选用2种食材”可得:土润选用金针菇和水蜜桃,即C项正确。
第(2)题:
本题题干的问题中给出了新事实:“水仙选用土豆”,故从这一事实出发。
结合上题分析可知,水仙:土豆→┐木耳∧┐火腿。根据题干信息“要求每种食材只能有2人选用,每人又只能选用2种食材”可知,金粲:木耳∧火腿,故B项正确。
综上,可得表3-11:
表3-11
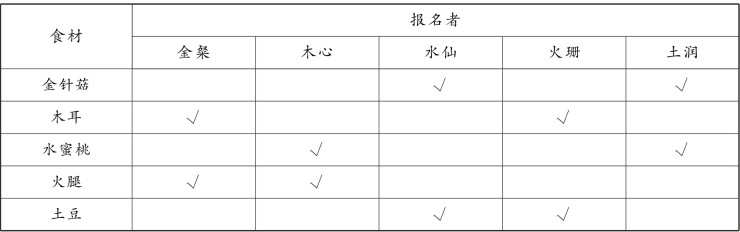
【答案】(1)C;(2)B
例35 甲、乙、丙、丁、戊和己6人围坐在一张正六边形的小桌前,每边各坐1人。已知:
(1)甲与乙正面相对。
(2)丙与丁不相邻,也不正面相对。
如果己与乙不相邻,则以下哪项一定为真?
A.如果甲与戊相邻,则丁与己正面相对。
B.甲与丁相邻。
C.戊与己相邻。
D.如果丙与戊不相邻,则丙与己相邻。
E.己与乙正面相对。
【解析】题干中有以下信息:
(1)甲与乙正面相对。
(2)丙与丁不相邻,也不正面相对。
(3)己与乙不相邻。
由题干信息(1)可得图3-14:
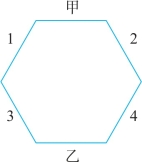
图3-14
由题干信息(2)可知,丙和丁的座次只可能是:1和2、3和4、4和3、2和1。
由题干信息(3)可知,己只能在1或2。故丙和丁的座次只可能为:3和4、4和3,如图3-15和图3-16所示:
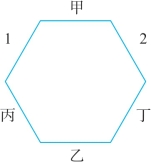
图3-15
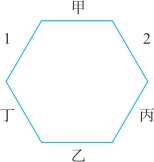
图3-16
由以上分析可排除B、C、E三项。
此时,将A、D两项的前件作为已知条件进行分析:
A项,若甲与戊相邻,则己与丁可能正面相对,也可能不正面相对,故排除此项。
D项,若丙与戊不相邻,则戊只能在丙的对面,则己与丙相邻,故此项正确。
【答案】D
定式2二难推理式
在综合演绎推理题中,当已知条件中出现两个或两个以上的假言判断时,考虑使用二难推理推出事实。
这类已知条件常见有两种:
(1)一真一假式。
如果已知条件中两个假言判断的前件分别为A和非A,即一真一假,考虑使用二难推理公式。
例如:
已知:①若甲入选,则乙入选。②若甲不入选,则乙也入选。
分析:甲→乙,┐甲→乙。由二难推理公式可知,乙为真,即乙入选。
(2)前后相同式。
两真:如果已知条件中出现两个假言判断,其中一个假言判断的前件为“A”,另外一个假言判断的后件也为“A”。此时有两种解法:①将这两个条件直接串联;②将后件为“A”的假言判断逆否,就可能使用二难推理。
两假:如果已知条件中出现两个假言判断,其中一个假言判断的前件为“非A”,另外一个假言判断的后件也为“非A”。此时有两种解法:①将这两个条件直接串联;②将后件为“非A”的假言判断逆否,就可能使用二难推理。
例如:
已知:①┐A→B。②B→C。③C→A。
分析:观察条件②、③,发现条件②的后件为“C”,条件③的前件也为“C”。将后件为“C”的条件②逆否可得:┐C→┐B,再由条件①逆否可得:┐B→A。
故有:┐C→┐B→A,结合条件③C→A,由二难推理公式(3)可得:A必然为真。
【注意】这种题有时候也可以直接串联。将条件①、②、③串联可得:┐A→B→C→A。可见,由“┐A”出发推出了矛盾,所以“┐A”不成立,因此,“A”必然为真。
典型例题
例36 第23届“沃边得”艺术节在北京举行。现有四个人张珊、李思、王伍、赵陆是最佳导演、最佳主角、最佳配角、最佳编剧的有力竞争者。评选结果出来后,发现每人恰好赢得了一个奖项。
已知:
①若张珊不是最佳导演,则李思是最佳主角。
②若李思是最佳主角,则赵陆是最佳编剧。
③若王伍或赵陆是最佳配角,则李思也是最佳配角。
④若赵陆是最佳编剧,则张珊是最佳导演。
根据以上信息,可以得出以下哪项?
A.张珊是最佳主角。 B.张珊是最佳编剧。 C.李思是最佳配角。
D.王伍是最佳导演。 E.赵陆是最佳编剧。
【解析】观察条件②、④,发现条件②的后件为“赵陆是最佳编剧”,条件④的前件也为“赵陆是最佳编剧”。
将后件为“赵陆是最佳编剧”的条件②逆否可得:┐赵陆是最佳编剧→┐李思是最佳主角。再由条件①逆否可得:┐李思是最佳主角→张珊是最佳导演。
串联可得:┐赵陆是最佳编剧→┐李思是最佳主角→张珊是最佳导演。
联合条件④:赵陆是最佳编剧→张珊是最佳导演。由二难推理公式(3)可知,张珊是最佳导演。
由条件③可知,若王伍或赵陆是最佳配角,则李思也是最佳配角,与题干“每人恰好赢得了一个奖项”矛盾,故王伍、赵陆均不是最佳配角,又由于张珊是最佳导演,故最佳配角只能是李思。
【答案】C
定式3是B不C式
关系推理(综合推理)题中,常有这样的条件:A是B,从而得到A不是C,老吕称之为“是B不C式”。
例如:
若张珊是南京人(A是B),则张珊肯定不是北京人(A不是C)。
再如:
条件①:如果李研究员来自复旦大学,则张教授来自北京大学。
条件②:如果张教授不是来自清华大学,则李研究员来自中科大。
分析:若张教授来自北京大学,可知,张教授不是来自清华大学。
因此,条件①和②可进行搭桥串联,可得:李研究员来自复旦大学→张教授来自北京大学→张教授不是来自清华大学→李研究员来自中科大。
从而推出了矛盾,故李研究员不是来自复旦大学。
典型例题
例37 因业务需要,某公司欲将甲、乙、丙、丁、戊、己、庚7个部门合并到丑、寅、卯3个子公司。已知:
(1)一个部门只能合并到一个子公司。
(2)若丁和丙中至少有一个未合并到丑公司,则戊和甲均合并到丑公司。
(3)若甲、己、庚中至少有一个未合并到卯公司,则戊合并到寅公司且丙合并到卯公司。
根据上述信息,可以得出以下哪项?
A.甲、丁均合并到丑公司。
B.乙、戊均合并到寅公司。
C.乙、丙均合并到寅公司。
D.丁、丙均合并到丑公司。
E.庚、戊均合并到卯公司。
【解析】本题的已知条件以假言判断为主,是一道综合演绎推理题,其解题方法必然会以串联推理、二难推理等知识为基础。
题干已知信息如下:
①┐丁丑∨┐丙丑→戊丑∧甲丑。
②┐甲卯∨┐己卯∨┐庚卯→戊寅∧丙卯。
因为:甲丑→┐甲卯(是B不C式)。
由②可知:③┐甲卯→戊寅∧丙卯。
故由①、③串联可得:┐丁丑∨┐丙丑→戊丑∧甲丑→┐甲卯→戊寅∧丙卯。
故,若有“┐丁丑∨┐丙丑”,可推出“戊丑”且“戊寅”,与题干“一个部门只能合并到一个子公司”矛盾。故“┐丁丑∨┐丙丑”为假,即有:“丁丑∧丙丑”为真。
【答案】D
定式4两两互斥式
关系推理(综合推理)题中,常有构成互斥关系的条件。具体又可分为以下两种:
(1)两个条件之间形成互斥。
例如:
条件①:张珊打过三场比赛。
条件②:南京人仅打过两场比赛。
可得:张珊不是南京人。
再如:
条件①:张珊学历最高。
条件②:山东人的学历比河南人低。
可得:张珊不是山东人。
(2)同一个条件内部两两互斥。
例如:
张珊和南京人一起吃过饭。说明张珊不是南京人。
张珊、南京人、作家一起吃过饭。说明张珊、南京人、作家两两互斥,可推出三个事实:张珊不是南京人、张珊不是作家、南京人不是作家。
典型例题
例38 赵嘉、钱宜和秦玲三个同学共报名六门注册会计师考试课程:会计、税法、经济法、财务管理、审计、公司战略。每人报名两门,且三人报的科目均不相同。他们的情况如下:
(1)报名经济法的同学和报名税法的同学是室友。
(2)秦玲最年轻。
(3)赵嘉经常和报名财务管理的同学以及报名税法的同学交流学习心得。
(4)报名财务管理的同学的年纪比报名会计的同学的年纪大。
(5)秦玲、报名审计的同学和报名会计的同学经常下自习后一起去吃晚饭。
根据以上条件,请判断以下哪项是正确的?
A.赵嘉报名会计和审计。
B.秦玲报名经济法和财务管理。
C.钱宜报名公司战略和经济法。
D.秦玲报名税法和公司战略。
E.赵嘉报名经济法和审计。
【解析】条件(1)内部形成互斥关系,故有:(6)报名经济法的同学和报名税法的同学不是同一人。
条件(2)和条件(4)形成互斥关系,故有:(7)秦玲没有报名财务管理。
条件(3)内部形成互斥关系,故有:(8)赵嘉、报名财务管理的同学、报名税法的同学两两互斥。
条件(4)内部形成互斥关系,故有:(9)报名财务管理的同学和报名会计的同学不是同一人。
条件(5)内部形成互斥关系,故有:(10)秦玲、报名审计的同学、报名会计的同学两两互斥。
由条件(7)、(8)可知,秦玲、赵嘉均没有报名财务管理,故钱宜报名财务管理,再由条件(8)可知,钱宜没有报名税法,又由条件(9)可知,钱宜没有报名会计。
又由条件(8)可知,赵嘉没有报名税法,故秦玲报名税法。
又由条件(7)、(10)可知,秦玲没有报名财务管理、审计、会计。故报名会计的是赵嘉。
此时可得表3-12:
表3-12
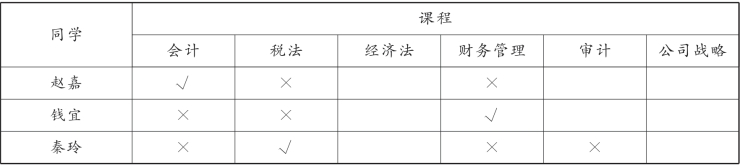
由条件(10)可知,报名会计、审计的同学不是同一人,所以赵嘉没有报名审计,故报名审计的是钱宜。
由条件(6)可知,秦玲没有报名经济法。根据题干信息“每人报名两门,且三人报的科目均不相同”可知,秦玲报名公司战略,赵嘉报名经济法。
综上,可得表3-13:
表3-13
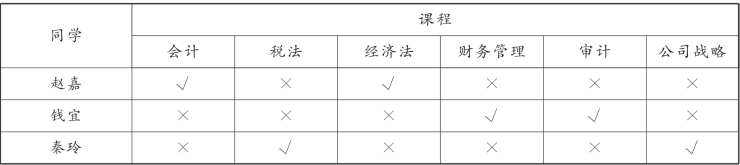
【答案】D
定式5情况分类式
当从已知条件中无法确定事实,但能确定某一元素的情况较少时,可按这一元素的情况进行分类讨论。
例如:
已知张珊是南京人或北京人。可分别假设她是南京人、北京人,按这两种情况进行分类讨论。
典型例题
例39 某海军部队有甲、乙、丙、丁、戊、己、庚7艘舰艇,拟组成两个编队出航,第一编队编列3艘舰艇,第二编队编列4艘舰艇。编列需满足以下条件:
(1)航母己必须编列在第二编队。
(2)戊和丙至多有一艘编列在第一编队。
(3)甲和丙不在同一编队。
(4)如果乙编列在第一编队,则丁也必须编列在第一编队。
如果丁和庚在同一编队,则可以得出以下哪项?
A.甲在第一编队。 B.乙在第一编队。 C.丙在第一编队。
D.戊在第二编队。 E.庚在第二编队。
【解析】题干已知“丁和庚在同一编队”,但无法确定丁和庚具体在第几编队,因此,可按两种情况进行分类讨论。
假设丁和庚在第一编队,由条件(3)可知,甲和丙不在同一编队,又知“第一编队有3艘舰艇”,所以第一编队的最后一个位置给甲或丙,则戊、乙、己都在第二编队。
假设丁和庚在第二编队,由条件(1)可知,己也在第二编队,又由条件(3)可知,甲和丙不在同一编队,又由于“第二编队有4艘舰艇”,所以,第二编队的最后一个位置给甲或丙,则乙在第一编队,再由条件(4)可知,丁也必须编列在第一编队,与假设矛盾,故丁和庚不可能在第二编队。
因此,第一种假设成立,戊在第二编队。
【答案】D
例40 某宿舍住着四位研究生,分别是四川人、安徽人、河北人和北京人。他们分别在中文、国政和法律三个系就学。其中:
Ⅰ.北京籍研究生单独在国政系。
Ⅱ.河北籍研究生不在中文系。
Ⅲ.四川籍研究生和另外某个研究生同在一个系。
Ⅳ.安徽籍研究生不和四川籍研究生同在一个系。
由以上条件可以推出四川籍研究生所在的系为:
A.中文系。 B.国政系。 C.法律系。
D.中文系或法律系。 E.无法确定。
【解析】由条件Ⅰ、Ⅱ可知,河北籍研究生不在中文系、不在国政系,故有:①河北籍研究生在法律系。
由条件Ⅰ可知,四川籍研究生不在国政系,只能在中文系或者法律系。
假设四川籍研究生在中文系,由条件Ⅲ可知,还有一名研究生在中文系,由条件Ⅰ和①可知,这名研究生不是北京籍和河北籍,故只能是安徽籍,与条件Ⅳ矛盾,所以四川籍研究生不在中文系。
故四川籍研究生只能在法律系。
【答案】C
