药物消除动力学模型
从生理学上看,体液被分为血浆、细胞间液及细胞内液几个部分。为了说明药动学基本概念及规律,现假定机体为一个整体,体液存在于单一空间,药物分布瞬时达到平衡(一室模型)。问题虽然被简单化,但所得理论公式不失为临床应用提供了基本规律。按此假设条件,药物在体内随时间的变化可用下列基本通式表达:
![]()
式中c为血药浓度,常用血浆药物浓度;k为常数;t为时间。
由于c为单位血浆容积中的药量(A),故c也可用A代替:dA/dt=kcn(n=0,为零级动力学;n=1,为一级动力学)。药物吸收时c(或A)为正值,消除时c(或A)为负值。
(一)零级消除动力学
单位时间内体内药物按照恒定量消除,称为零级动力学消除,又称恒量消除。公式为
![]()
当n=0时,-dc/dt=KC0=K(为了和一级动力学中消除速率常数区别,用K代替k)。其药时曲线的下降部分在半对数坐标上呈曲线(图2-6),称为非线性动力学。体内药物浓度远超过机体最大消除能力时,机体只能以最大消除速率将体内药物消除。消除速率与C。大小无关,因此是恒速消除。例如饮酒过量时,一般常人只能以每小时10 mL。乙醇恒速消除。当血药浓度下降至最大消除能力以下时,则按一级动力学消除。按零级动力学消除的药物,其t1/2不是一个恒定的值,可随血药浓度变化而变化。
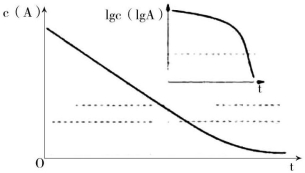
图2-6 药物在体内消除过程的药-时曲线
(二)一级消除动力学
单位时间内体内药物按恒定的比例消除,称为一级动力学消除,又称恒比消除。公式为:
![]()
当n=1时,dc/dt=kec=kec(k用ke表示消除速率常数)。当机体消除能力远高于血药浓度时,药物从体内的消除按一级动力学消除。进入体内的药物大多是按一级动力学消除的,药物的t1/2是恒定的。(https://www.daowen.com)
Ct=Coe-ket
取自然对数,
lnCt=lnCo-ket
换算成常用对数,
![]()
![]()
当Ct=1/2Co时,t为药物半衰期(t12):
![]()
可见,按一级动力学消除的药物半衰期与C大小无关,是恒定值。体内药物按瞬时血药浓度(或体内药量)以恒定的百分比消除,单位时间内实际消除的药量随时间递减。消除速率常数(ke)的单位是h-1,它不表示单位时间内消除的实际药量,而是体内药物瞬时消除的百分率。例如,ke=0.5 h-1不是说每小时消除50%(如果t1/2=1小时则表示每小时消除50%)。按t1/2=0.693/ke计算,t1/2=1.39小时,即需1.39小时后才消除50%。再按计算,1小时后体内尚存60.7%。绝大多数药物都按一级动力学消除。这些药物在体内经过t时后尚存
At=AoC-ket,ko=0.693/t1/2
T以t1/2为单位计算(即t=n×t1/2),则:
![]()
当n=5时,At≈3%A。即经过5个t1/2后体内药物已基本消除。与此相似,如果每隔一个t1/2给药一次(Ao),则体内药量(或血药浓度)逐渐累积,经过5个t1/2后,消除速率与给药速率相等,达到稳态。
