连续多次用药的血药浓度变化
临床治疗常需连续给药以维持有效的血药浓度。在一级动力学药物中,开始恒速给药时,药物吸收快于药物消除,体内药物蓄积。按计算约需5个t1/2达到血药稳态浓度(CXS)(图2-8),此时给药速度(RA)与消除速度(RE)相等。
![]()
可见,Cxs随给药速度(RA=Dm/,)快慢而升降,到达Cxs的时间不因给药速度加快而提前,它取决于药物的是ke或t1/2。据此,可以用药物的keVd或CL计算给药速度,以达到所需的有效药物浓度。
静脉恒速滴注时,血药浓度可以平稳地到达Cxs,分次给药虽然平均血药浓度上升与静脉滴注相同,但实际上血药浓度上下波动(图2-8)。间隔时间越长波动越大。
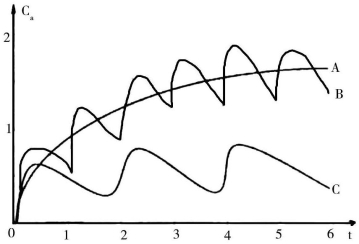
图2-8 连续恒速给药时的时量曲线
约经5个半衰期血药浓度达到稳态,给药间隔越短,血药浓度波动越小;给药剂量越大,血药浓度越高。A.静脉滴注,Dm/t1/2;B.肌内注射,Dm/t1/2;C.肌内注射,1/2 Dm/2t1/2(Dm是维持剂量)
药物吸收达到CXS后,如果调整剂量需再经过5个t1/2。方能达到需要的Cxs。
在病情危重需要立即达到有效血药浓度时,可于开始给药时采用负荷剂量(loading dose,D1),即每隔一个t1/2给药一次时,采用首剂加倍剂量的D1可使血药浓度迅速达到Cxs。
理想的给药方案应该是使Cxs-max略小于最小中毒血浆浓度(MTC)而CXS-max略大于最小有效血浆浓度(MEC),即血药浓度波动于MTC与MEC之间的治疗窗,这一Dm可按下列公式计算:(https://www.daowen.com)
Dm=(MTC-MEC)Vd
D1=ASS=1.44t1/2RA=1.44t1/2Dm/τ,τ可按一级消除动力学公式推算得τ=(lgCo/c τ)×2.303/K τ,令Co=MTC,C τ=MEC。
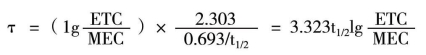
因此可以根据药物的MTC及MEC计算D1,Dm及τ。注意此时τ≠t1/2,D1≠2Dm(图2-9)。
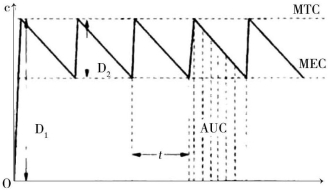
图2-9 负荷剂量、维持剂量、给药间隔与血药浓度的关系
此外,在零级动力学药物中,体内药量超过机体最大消除能力。如果连续恒速给药,RA﹥RE,体内药量蓄积,血药浓度将无限增高。停药后消除时间也较长,超过5个t1/2。
临床用药可根据药动学参数如Vd、CL、ke、t1/2及AUC等按以上各公式计算剂量及设计给药方案,以达到并维持有效血药浓度。除了少数t1/2特长或特短的药物以及零级动力学药物外,采用每一个半衰期给予半个有效量并将首次剂量加倍是有效、安全、快速地给药方法。
有些药在体内转化为活性产物,则需注意此活性产物的药动学,如果活性产物的消除是药物消除的限速步骤,则应按该产物的药动学参数计算剂量及设计给药方案。
