2.2.1 爆炸作用下壳体破裂刚塑性模型
对于柱形单中心管抛撒结构，其爆炸抛撒结构截面如图2-3所示。壳体在内压作用下，壳体扩张。其受力状态如图2-4所示，壳体内表面由燃料传递的压力为2P，外表面受到环境空气压力为1P。
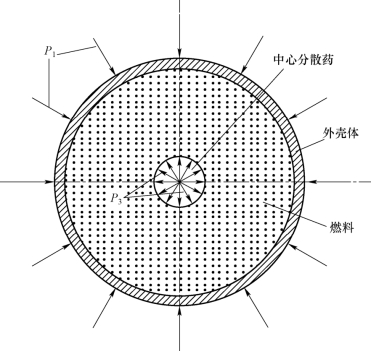
图2-3 爆炸抛撒结构截面图
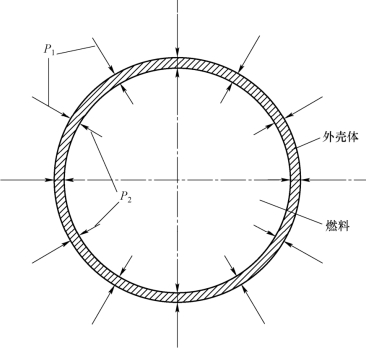
图2-4 壳体受力情况
对壳体破裂进行简化，并引入假设条件：
（1）壳体一维径向运动。
（2）壳体在变形过程中，应力波已在其中多次反射，即不讨论应力波的传播作用。
（3）由于所研究问题为壳体的大变形问题，其弹性阶段可不考虑，采用不可压缩理想刚塑性材料模型。
由质量守恒条件可得
式中，ρ为流体密度；u为流速，r为流体半径。由问题轴对称性可知，单元体四角不发生角应变，切应力均为零，如忽略体积力，则只受面力σr、σθ和σz。由于只有r方向有质量通过，因此只有r方向有动量流入/流出，根据动量守恒条件可得
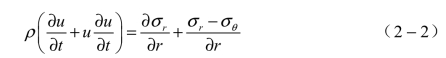
采用米塞斯（Mises）屈服准则来判断壳体材料的失效，其表达式为
式中，σ1、σ2和σ3为主应力；
为材料的动态屈服应力。在柱面坐标系的轴对称问题中，三个正应力σr、σθ、σz就是三个主应力，按照平面应变条件有
米塞斯屈服准则可写为
利用连续方程、运动方程和米塞斯屈服准则方程（2-5）的边界条件就可以解出壳体破裂半径和破片初始速度，得到壳体内部的应力分布：
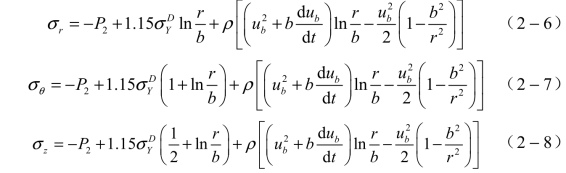
在通常情况下，球腔内壁处的压力P2远大于屈服应力
。因此。除非P2降到
值或更低，内壁处的σr和σθ都处于压应力状态：
随着r的增加，由式（2-7）可知，σθ的压应力值减小。设在rh=（c-h）处，σθ=0；则在r＞rh处，σθ≥0，即为拉应力。这里c是厚壁壳体的外半径，h是从外壁量起的距离。
当压应力区消失而裂纹穿透到内壁时，壳体才会发生破碎。σθ由拉应力转为压应力的界面位置rb，即h值，可由σθ=0的条件给出如下公式：
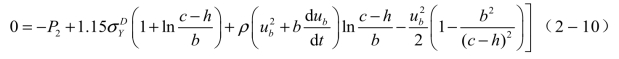
而σθ为压应力区消失的条件是h=c-b，由此可见，只有当Pb值随时间下降到
时，管状壳体才会破碎。
对壳体外壁，将r=c和σr=-P1代入式（2-6）得到内壁质点速度随时间变化的表达式：
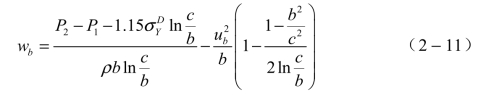
式中，wb表示壳体内壁的加速度，同时也相当于膨胀阶段燃料环外壁的加速度；P1是空气对壳体外壁上的压力；P2是通过燃料的壳体内壁的压力；b、c分别为壳体在变形过程中的内半径、外半径；ub为壳体的质点速度，并等于膨胀阶段外壁火燃料粒子的速度。
综上，可以追踪壳体的运动过程，记录壳体膨胀全过程，可以得到壳体破碎时初始飞行速度。