7.4.1 多传感器信息融合技术
7.4.1.1 基本概念与模型
美国三军组织实验室联合理事会最早提出了多传感器信息融合技术的概念,具体定义为:信息融合就是一种多层次、多方面的处理过程,包括对多源数据进行检测、相关、组合和估计,从而提高状态和身份估计的精度,以及对战场态势和威胁的重要程度进行适时完整的评价。
多源信息数据融合技术可以将多源异类传感器的数据有机结合起来,从而可以提高系统可信度,增强系统鲁棒性,降低数据误差,拓展系统功能和降低系统成本,得到广泛关注和深入研究,该项技术的应用范围也很快从军用领域扩展到环境监控、工业控制、交通管理、电子商务等工业和民生领域。
按照数据抽象层次不同,通常可以将数据融合结构分为像素级融合、特征级融合和决策级融合三个层次。
(1)像素级融合又称为数据级融合,是指对传感器原始数据直接进行的融合处理。该融合方式可以保留足够多的原始特征信号,从而可以实现较为精细化的融合,由于原始数据包含的噪声及非特征信号较多,因此要求融合算法具有较强的计算能力和特征辨识能力。
(2)特征级融合方法要求首先对传感器原始数据进行处理,获取原始数据中的特征数据,再对特征数据进行融合处理。特征级融合是中间层次的融合方法。由于提前完成了信号特征值提取,因此对于传感器一致性的要求较低,同时计算量下降,计算效率相对像素级融合有所提高。
(3)决策级融合是高层次融合方法,该层次的融合算法实现对各个测试节点初步决策进行融合,形成最优化决策输出。该层次的融合摆脱了对传感网络特性的依赖,具有较高的容错特性,并具有运算工作量少、实时性高等优点。但是对于前期决策的依赖性增高,要求测试节点具有较高的预处理能力。
根据数据融合环节在信息处理过程中的位置,可以将数据融合系统分为集中式融合、分布式融合和混合式融合,相应的体系结构如图7-12所示。
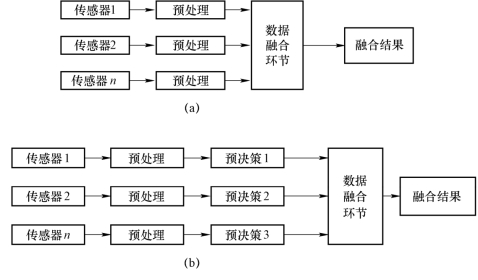
图7-12 信息融合体系结构示意图
(a)集中式融合;(b)分布式融合
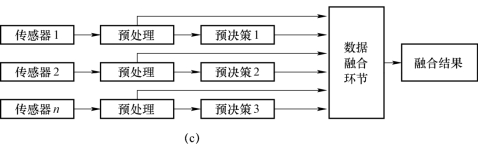
图7-12 信息融合体系结构示意图(续)
(c)混合式融合
7.4.1.2 常用信息融合算法分析对比
多传感器信息融合技术是一门新兴的多学科交叉技术,研究领域涉及数据统计、信号处理、人工智能等,同时应用范围也覆盖了科研、军事、工业、交通等领域,因此形成了多种原理、特征和应用均不相同的数据融合算法。目前研究和应用均较为广泛的数据融合算法包括基于贝叶斯理论的数据融合算法、基于D-S理论的数据融合算法、基于模糊集理论的数据融合算法、基于神经网络的数据融合算法以及基于滤波理论的数据融合算法。
(1)加权平均法。加权平均法的数学实现过程为:设用n个同质传感器对某目标进行检测,传感器节点i的测试数据为xi。根据特定的加权系数wi对传感器组的检测数据进行加权求和,可以得到加权平均融合结果:

其中,加权系数wi满足

加权平均法是最简单的数据融合方法,计算量极小,可以实现数据实时融合处理。加权平均法的技术核心在于选择最优加权系数矩阵。加权系数体现了测试数据对于总体结果的贡献程度。当使用同类型传感器对线性系统进行观测时,加权系数可以进一步简化为wi=1/n;但是在传感器特性不同和被测系统非线性条件下,需要首先对测试系统和传感器特性进行分析,采用经验方法或者学习方法获得最优加权系数,此时系统趋于复杂。
(2)神经网络法。神经网络法是主要进行数据处理的计算方法。在计算空间中建立一系列功能简单的神经元,神经元之间通过特定权值进行多对多互连,采用逻辑处理的方法完成数据加权合成;连接权值和处理逻辑能够通过学习方法不断进化,并形成记忆和判断,最终实现多数据的快速融合处理。神经网络方法具有自学习和自适应的能力,经过足够多的学习过程之后可以对复杂和非线性的数据进行高效处理。但是该方法需要一定的学习时间和学习样本,因此适用于长期稳定在线工作,不适用于实现快速检测。
(3)卡尔曼滤波算法。卡尔曼滤波算法是一种基于递推和误差估计思想的数据处理方法。该方法根据前一状态的估计误差和数据检测值对当前时刻数据统计特性进行最优估计,从而提供当前检测值的滤波(修正)计算值。基于卡尔曼滤波算法的数据融合方法本质是计算多个传感器数据的加权平均值,各个传感器数据的权重与其检测方差成反比。由于采用递推的计算思想,因此该方法具有良好的计算特性,便于算法编程实现,并具有较高的计算实时性和足够的计算精度,因此得到了广泛的研究与应用。
(4)模糊集理论法。模糊集理论把传统集合概念中的隶属关系进行模糊化,使元素对特征集合空间的隶属度由{0,1}扩展为[0,1],从而形成了新的集合概念和运算规则。模糊集理论法根据数据特征建立模糊论域,并根据一定的模糊规则和隶属度函数对数据进行模糊集计算,获得数据融合输出值。该方法采用模糊变量对系统进行描述,具有一定的智能性,适用于非线时变系统分析处理;但是模糊化过程中模拟规则和隶属度函数主要基于经验建立,对于计算精度有较大影响,同时计算量和计算精度之间存在矛盾。
浓度检测方法需要具备良好的测试精度和测试速度,同时测试装置应满足低功耗小体积的要求,因此要求融合算法也具有良好的速度、精度和较小的系统资源开销。根据以上要求,从计算资源开销、运算量大小、计算实时性、是否需要较大的运算资源等方面对以上常用数据融合算法进行特性对比,形成统计对比,如表7-5所示。
表7-5 常数数据融合算法特征对比
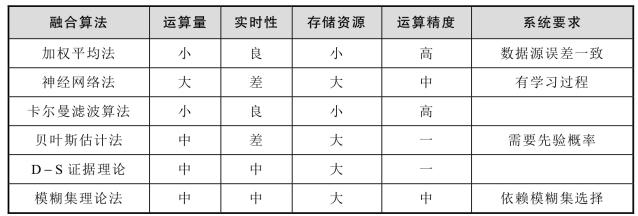
根据表7-5可知,加权平均法和卡尔曼滤波算法基本满足项目需求。但是由于声—电复合检测方法中声学传感器和电学传感器特性相差较大,采用加权平均法时需要额外计算最优加权系数,计算量较大,因此选择采用卡尔曼滤波算法进行多传感器数据融合。
