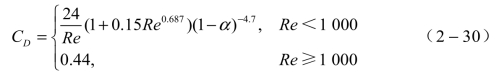2.2.3 燃料抛撒形貌发展模型
初始破碎形成的燃料块在空气中运动，和空气产生相互作用，在阻力作用下，燃料块发生二次破碎。由于颗粒之间碰撞而发生破碎的情况很少，且过程复杂，所以忽略燃料块之间的碰撞，主要考虑燃料块与空气的作用。在空气的作用下，颗粒主要受到气动剥离和燃料蒸发效应影响，这些效应使得燃料块的尺寸逐渐减小。假设燃料块为球形，燃料块的特征尺度取其平均半径l，则燃料块的破碎效应中剥离和蒸发分别采用剥离模型和蒸发模型描述。
2.2.3.1 剥离、蒸发效应模型
剥离方程：燃料块或液滴剥离效应主要由其与空气相对运动引起的摩擦等效应引起，其剥离速率可以按下式表示：
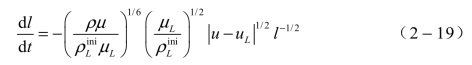
式中，ρ、
分别是空气、燃料介质的密度；μ、μL分别是空气、燃料介质黏性系数；μ、μL分别是空气、燃料介质的速度；l为燃料液滴的平均半径。
蒸发方程：在空气的作用下，燃料块的破碎主要效应有气动剥离和燃料蒸发雾化。根据Eidelman蒸发模型，假设液滴的整个表面均匀蒸发，液滴的温度在蒸发过程中保持恒定，其蒸发速率如下：
式中，
是燃料颗粒或液滴的密度；kGAS是空气的热传导率；Nu是Nusselt数；T、TL分别是空气和燃料颗粒或液滴的温度（K）；L是燃料液滴的蒸发热（J/kg）；颗粒温度、空气温度和声速是常数，l为燃料液滴的平均半径。
剥离效应和蒸发效应，可以得到燃料颗粒或液滴体积变化量为两者之和，即
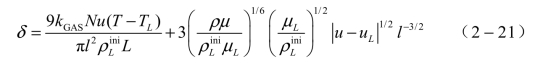
2.2.3.2 液滴、颗粒的粒径变化模型
采用破碎函数对燃料环破碎后的初始燃料颗粒粒度分布进行描述：
式中，（di，di+1）为颗粒粒径分布区间；m为颗粒粒径的分布区间个数；n为颗粒总数；
为分布在同一粒径区间的颗粒个数，此处设为各粒径区间内分布颗粒个数相同。
粒子直径计算如下：
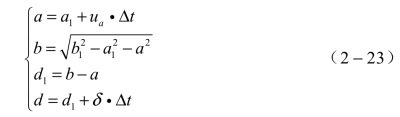
式中，a1为燃料环的初始内半径；b1为燃料环的初始外半径；d1为粒子的初始直径；d为随时间变化的粒子直径。初始碎片的宽度与压实层的厚度有关。在该模型中，以燃料破碎前的厚度近似为初始燃料碎片的最大尺寸。
2.2.3.3 液滴、颗粒的粒径运动模型
在忽略燃料颗粒或液滴之间碰撞时，燃料颗粒或液滴的运动可以采用单颗粒运动动力学模型。在单颗粒动力学模型中，不考虑颗粒相对连续相流体的影响，也不考虑颗粒间的相互作用和颗粒脉动，它是一种单向耦合模型，只考虑单个颗粒在连续相流体中的受力和运动。单颗粒在流场中受力如图2-6所示。
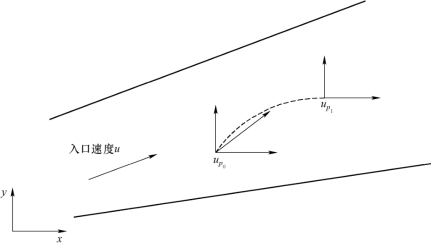
图2-6 单颗粒在流场中的受力及运动
在拉格朗日坐标系中，单颗粒运动方程的一般形式为
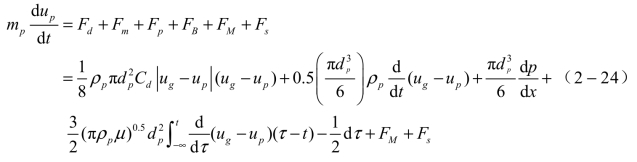
式中，右端为颗粒运动的阻力、附加质量力、压力梯度力、Basset力、Magnus力和Saffman力等。在实际应用中，大多数情况下只考虑阻力和重力，可忽略其他力的作用。
流场曳力（阻力）和阻力系数：颗粒悬浮于流体中的两相流动的主要特征是颗粒与流体的速度和速度不相等，因此两相间存在相互作用力和热交换。所谓阻力是颗粒在静止流体中作匀速运动时流体作用于颗粒上的力。如果来流是完全均匀的，那么颗粒在静止流体中运动所受的阻力，与运动着的流体绕球体流动作用于静止颗粒上的力是相等的。在爆炸抛撒颗粒群的问题中，当颗粒由稠密流逐渐转变为稀疏流时，此时颗粒间的相互作用力可忽略不计，而流场曳力将对颗粒的运动起着至关重要的作用。
颗粒在黏性流体中运动时，流体作用于球体上的阻力由压差阻力和摩擦阻力组成，习惯上把阻力Fd的表达式写成
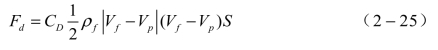
式中，Vf和ρf分别流体的速度和密度；Vp为颗粒的速度；S为颗粒的迎风面积，S=
；CD为阻力系数。
阻力系数可以从纳维—斯托克斯（Navier-Stokes）方程的数值中获得。但由于球形颗粒表面的附面层非常复杂，只有极少数特殊情况可从方程组导出计算式。目前，阻力系数主要依靠实验来确定，从而选择合适的阻力系数公式进行计算模拟。颗粒的阻力系数是与颗粒雷诺数紧密相关的，计算如下：
Clift等总结、分析了在不同雷诺数区间的理论研究和实验数据，推荐了适用于雷诺数范围较大的分断表达的曳力系数经验公式：
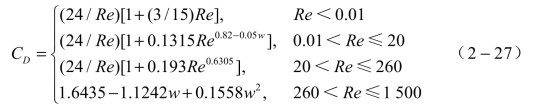
简单常用的表达式为
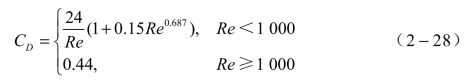
颗粒群阻力系数修正：如果流场中同时存在多个颗粒，颗粒之间就会发生相互作用。一种形式的相互作用是颗粒之间的直接碰撞，另一种形式的相互作用是通过颗粒尾流的间接作用，对颗粒的阻力造成显著影响。例如当颗粒一个跟着一个运动时，每个颗粒所受的阻力比单个颗粒运动所受阻力小很多。通过实验可以测定各种条件（不同的粒径，不同颗粒浓度等）下的表观阻力系数。
对于颗粒群的曳力系数，常用的计算方法为单颗粒的曳力系数CD与颗粒体积分数的函数的乘积：
体积分数F（α）的常用表达式为F（α）=（1-α）-4.7，其中α为空隙率。与单颗粒的曳力系数表达式相结合，则颗粒群的曳力系数可表示为
