6.3.1 基于经典ECAH云雾浓度计算模型
经典ECAH模型的基本推导过程如下。
6.3.1.1 理论假设
ECAH模型是多相物声波衰减的基础模型,其理论基础是守恒型流体动力学方程,该模型遵循以下假设条件:
(1)采用Avier-Stokes 形式的量守恒方程,同时忽略热应力的影响。
(2)声传播中,介质温度与压力与时间无关,衰减过程处于准稳态状。
(3)认为黏性系数和热传导系数为常数值。
(4)应力应变张量符合以下关系:
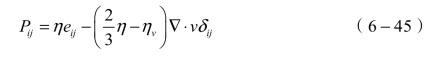
6.3.1.2 声场方程和波动方程
根据声场内振子的质量、动量和能量守恒关系,可以建立如下方程组:
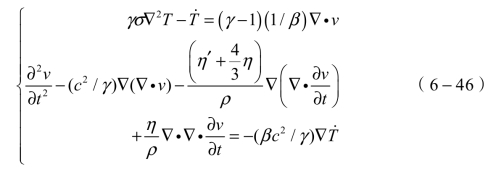
主要计算参数如下:
σ——导温系数,通过σ=τ/ρ0Cp计算,其中τ 为热导率;
Cv——定容比热;
γ——比热比,通过γ=Cp/Cv算;
β——热膨胀系数,通过β=-(1/ρ0)/(∂ρ/∂T)p计算;
c——声速。
将向量v写成标量势φ的梯度和矢量势A的旋度的和的形式,进一步给出波动方程:

这里的复波数kc、ks、kT别由下式给出:

式中,aL为纵波的声衰减系数。
6.3.1.3 边界条件
取声场内的一个球形颗粒作为研究对象,并假设颗粒间距较大,不发生复散射。当声波入射到颗粒表面时,由于存在反射作用和透射作用,因此在颗粒表面产生一组方向相对的压缩波,分别称为ϕc和φc′;由于颗粒与周围介质密度不同,则颗粒和周围介质在相同声压作用下的运动速度不同,形成相对运动,从而产生剪切波和;此外,由于波动作用在颗粒表面产生了热损失,将其等效为热波作用和。入射波在球形颗粒表面的损失模式如图6-2所示。
在球形颗粒的表面,根据轴对称原理可以建立关于速度、应力、温度等因素的边界条件如下:
![]()
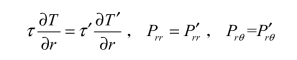
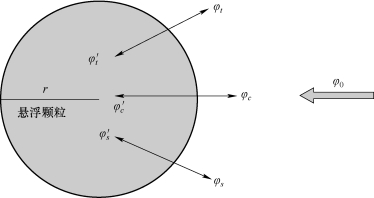
图6-2 入射波的损失模式
6.3.1.4 单颗粒散射系数
将边界条件代入波动方程,可以获得一个关于6个待定系数的线性方程组,该方程组实质上描述了在颗粒内部和周围介质的3种波动的势函数,其中包含待定系数An、Bn、Cn、![]() 为衰减系数,线性方程组表示如下:
为衰减系数,线性方程组表示如下:
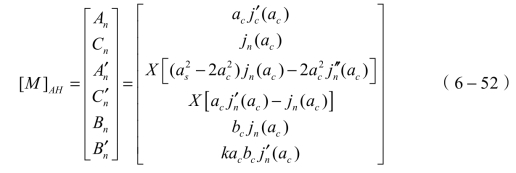
式中,![]() 和An为颗粒内部和外部的压缩波;
和An为颗粒内部和外部的压缩波;![]() 和Bn为颗粒内部和外部的热波;
和Bn为颗粒内部和外部的热波;![]() 和Cn为颗粒内部和外部的剪切波;ac和as分别是颗粒半径与压缩波和剪切波波数的乘积;jn为球贝塞尔级数;X为剪切模量,液体颗粒使用X=η,固体则采用X=μ/(jw)。
和Cn为颗粒内部和外部的剪切波;ac和as分别是颗粒半径与压缩波和剪切波波数的乘积;jn为球贝塞尔级数;X为剪切模量,液体颗粒使用X=η,固体则采用X=μ/(jw)。
上式对于理想单颗粒情况下的入射声波能量分解进行了全面的描述,但是由于热波和剪切波耗散较快,无法在X=μ/(jw)超声传感器的接收端形成有效贡献,因此,能够对测量产生意义的主要是压缩波。压缩波的势函数可以表示为
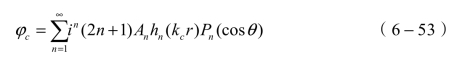
式中,Pn代表n阶勒让德多项式。
6.3.1.5 声场总体衰减系数
根据Epstein等的研究成果,在不考虑声波复散射的条件下,将单个颗粒的衰减情况推广到整个声场范围内,将上述波动方程在坐标系下求解,并按照球谐函数和球贝塞尔函数进行展开;将其代入固相颗粒和连续介质分界面上的边界条件,可以推导出6阶线性方程组,对该方程组进行求解,就可以得到一个n阶展开系数An。
可以得到颗粒相引起的超声波总的衰减系数α,其中总的能量损失与颗粒数目浓度成正比:

式中,φ为颗粒相在混合物中的体积浓度;kc表示超声波在连续介质中的波数;R表示颗粒的半径。
进一步考虑混合物中连续相的吸收作用,可以获得ECAH模型的最终结果(基于复波数表达形式):
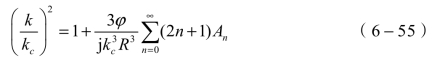
式中,k为超声在混合介质中的复波数;kc表示超声在连续介质中的波数;φ表示悬浮颗粒的体积浓度;R表示颗粒的半径。根据定义有
![]()
式中,ω为超声角频率;α和cs分别为超声波在混合介质中的衰减系数和声速。
根据计算得到的体积分数φ,根据式(6-64)可以得到其质量浓度:

