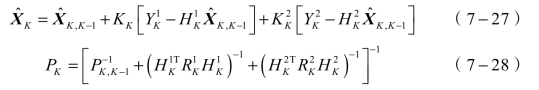7.4.2 基于卡尔曼滤波的数据融合模型
7.4.2.1 卡尔曼滤波算法
1960年和1961年，卡尔曼和布西提出了递推滤波算法，将状态变量引入到滤波理论，用消息与干扰的状态空间模型代替了协方差函数，将状态空间描述与离散数据刷新联系起来，不加推导地给出卡尔曼滤波算法的数学原理如下。
设动态系统的状态方程和检测方程分别为
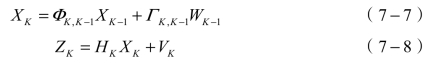
式中，XK是K时刻的系统状态，ΦK，K-1和ΓK，K-1是K-1时刻到K时刻的状态转移矩阵，ZK是K时刻的检测值，HK是检测系统的参数，WK和VK分别表示过程和检测的高斯白噪声。进一步预测：
状态估计：
滤波增益矩阵：
一步预测误差方差阵：
估计误差方差阵：
由上述推理可知，给定初值X0和P0，根据k时刻的观测值ZK，就可以递推计算得K时刻的状态估计
（K=1，2，…，N）。
根据卡尔曼滤波算法模型，可以得到其具体应用的计算步骤如下。
在t0时刻给定初值：
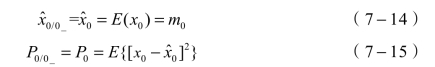
计算t0时刻的最优增益矩阵K0：
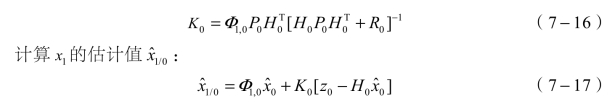
计算P1/0：
根据P1/0计算t1时刻的K1，根据K1计算x2的估计值x2/1。
重复以上步骤即可得到
，即得到后续时刻的估计数值。
根据上述计算过程可知，卡尔曼滤波算法主要采用递推计算，每次计算时只需保留前一次的数据，计算过程简单，计算量较小，因此适用于对计算速度有一定要求的场合，在在线检测等领域得到了广泛的应用。
但是卡尔曼滤波算法也存在受到计算系统字长影响，可能出现滤波器不收敛等情况，针对算法存在不足，研究者提出了限定记忆法、平方根滤波、渐消记忆滤波、自适应卡尔曼滤波（Adaptive Kalman Filtering，AKF）、抗野值滤波等改进型卡尔曼滤波算法，并在一定的科研和工程背景中取得了良好的使用效果。
7.4.2.2 基于卡尔曼滤波的声—电数据集中融合模型
根据卡尔曼滤波计算模型，在使用声场法和电场法分别进行燃料云雾浓度检测时，存在一组系统状态方程和两组检测方程：
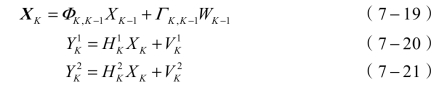
如果检测噪声方差矩阵R1和R2满足
为非奇异矩阵时，状态值X存在线性最小方差估计：
可以定义广义检测矢量为
广义检测方程为
根据经典卡尔曼滤波算法及最优融合估计定理，可以得到多传感器集中式融合算法的迭代算法为
