8.4.1 数据融合作用模式及算法分析研究
多传感器数据融合算法在信号检测、数据处理和系统控制等方面得到了广泛的研究和应用,并与传统数值计算、模糊理论等相结合,产生了多种各具特点的数据融合模式和算法。
8.4.1.1 数据融合作用模式
根据数据融合环节在信息处理过程中的位置,可以将数据融合系统分为集中式融合和分布式融合。集中式融合结构下,实现测试数据在数据融合中心集中对准、互联、估计、判断等行为的一次决策级输出。分布式融合结构下,单个传感器的测试数据预先处理,再将初步的结果送入后端融合中心,由后端融合中心实现最终的数据融合的决策输出。采用集中式融合体系时,系统基于全部完整数据进行信息融合,没有产生原始信息丢失,理论上可以获得最优的决策精度,但是对于系统计算资源要求较高,需要很大的存储和处理能力,系统生存能力较差。分布式融合系统克服了集中式结构中的缺陷,并且在容错性、实时性、稳定性和可扩展性等方面体现出极为明显的优势,因此得到广泛的采用。
采用双频超声进行云爆浓度检测时,需融合的数据量较小,但是对算法运行速度有一定的要求;此外,较为独特的应用背景对于硬件系统的体积、质量和功耗具有较为严格的限制,因此本课题组研究选择采用分布式融合模式。
8.4.1.2 数据融合算法
目前研究较为深入且应用较为广泛的数据融合算法包括加权平均方法、神经网络方法、卡尔曼滤波算法、贝叶斯估计法、D-S证据理论以及模糊集理论法等。上述算法各具特点,并在特定的领域获得了成功的应用。本研究从运算量、是否需要对以上常用数据融合算法进行特性对比,形成算法特征对比,如表8-1所示。
表8-1 常用数据融合算法特征对比表
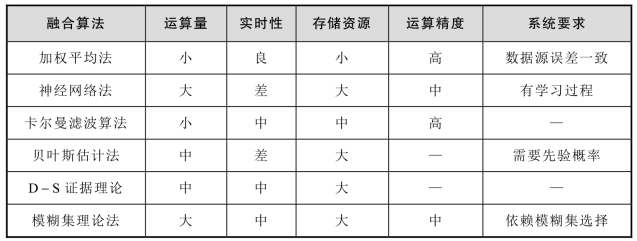
根据上述对比分析,本研究分别选择卡尔曼滤波算法和加权平均法作为分布式融合模式中底层和顶层的数据融合方法,建立一种基于上述两种算法的分布融合算法,该算法的总体作用模型如图8-7所示。
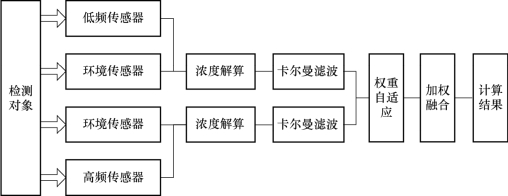
图8-7 分布式融合的最优加权数据融合算法示意框图
如图8-7所示,首先分别获得环境补偿后的低频超声测量结果和高频超声测量结果,然后根据第3章所述计算获得理论浓度值,采用卡尔曼滤波数据融合算法,依据高频和低频每个通道前一次的数据结果进行数据修正和融合。由于卡尔曼滤波算法只涉及存储以及参与计算的当前数据和前一次计算结果,计算资源需求较小,因此非常适合在底层节点端完成,从而分别获得特定频段下的浓度值C1和C2。在控制系统作用下,上述数据同步送入具备强大数据处理能力的顶层数据融合中心,在数据融合中心采用一种基于测量误差差值的自适应加权数据融合算法对C1和C2进行融合处理,最后获得可信度和精度均较为理想的最终浓度结果Ce。
