2.2.2 燃料环膨胀破裂模型
当壳体破碎前，燃料在中心分散装药爆轰产物驱动压力P3作用下向外运动，同时受到壳体约束力-P2作用；当壳体破碎后，燃料在中心分散装药爆轰产物的驱动下运动。由于壳体已破碎，壳体对燃料环的约束大大减小。在此假设当壳体破碎后，忽略壳体对燃料的影响，因此燃料环直接受到外部空气阻力和内部中心分散装药爆轰产物驱动力两者作用。图2-5给出了燃料环的受力状态。
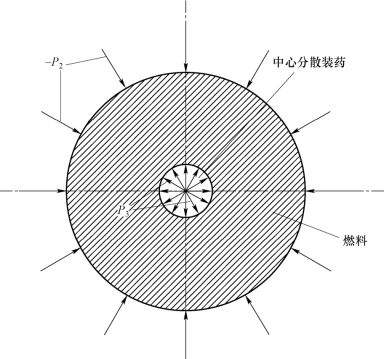
图2-5 燃料环受力状态
在燃料环的破裂过程中，被压缩的燃料被认为是不可压缩介质。燃料环的破坏过程和壳体破坏过程类似，在σθ压应力区消失，裂纹从外壁产生穿透内壁的情况下，燃料环发生断裂。
设定燃料环内半径a，外半径为b。从而得到
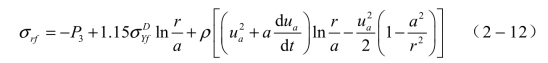
再代入平面应变条件，可得另外两个主应力：
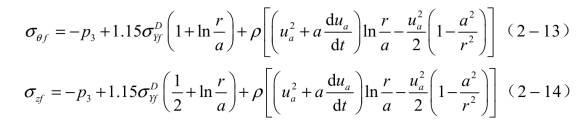
式中，σrf、σθf、σzf为燃料环内部在不同半径处的应力分布。在通常情况下，内壁处的压力远大于燃料屈服应力
。因此，当P3降到
值或更低，燃料环内壁处的σr和σθ都处于压应力状态：
随着r的增加，σθf的压应力值减小。设在rhf=（b-h）处，σθf=0；则在r＞rh处，σθf≤0，即为拉应力。这里b是燃料环的外半径，h是从燃料环外半径量起的距离。
得到σθf由拉应力转为压应力的界面位置rf，即h值，可由σθ=0的条件给出，如下式：
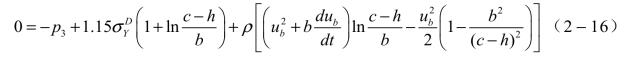
σθf为压应力之区域，消失的条件是h=b-a，由此可见，只有当P3值随时间下降到
值时，燃料环开始发生破碎。
燃料破碎成碎片的初始粒径和速度可以计算如下：
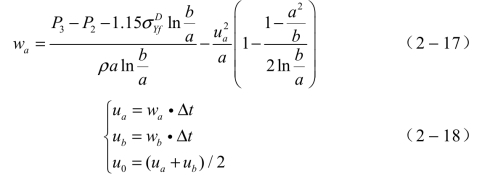
式中，wa表示燃料环内壁的加速度，wb代表的燃料环外壁的加速度；P3代表由分散装药爆炸产生的燃料环内壁受到的压力，P2代表燃料环外壁受到的空气产生的压力；a代表燃料环内半径，b代表燃料环的外半径；ua代表燃料环内壁的速度，ub代表燃料环外壁的速度；Δt为时间步长。进行颗粒的初速度计算。以燃料环膨胀至破裂前，燃料环内壁与外壁的速度的平均值近似作为燃料碎片u0的初速度。通过公式可以计算出颗粒的初速度，在该模型中，以膨胀后燃料环内速度和破裂前燃料环外速度的平均值作为燃料碎片u0的近似初速度。