5.3.2　粒径随机分布颗粒云雾模型数值计算

5.3.2　粒径随机分布颗粒云雾模型数值计算

设复合介质中的两相材料为均匀介质，且计算单元中均没有自由电荷，则云雾体单元的电势φ满足Laplace方程：

如图5-6所示，对于混合物中的第i个基本单元，其电场特性单元满足如下边界条件：设其上表面电位为ϕi，下表面电位为ϕi+1，且域中的第一类边界条件；4个侧面不存在电场的法向分量，即有∂ϕ/∂n=0，域中的第二类边界条件。

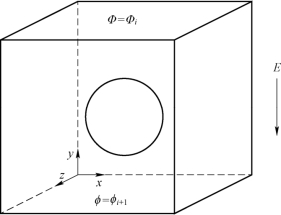
图5-6　基本单元边界条件示意图

利用有限元仿真软件ANSYS实现有限元的计算，计算时选用自适应网格划分方法。计算得到节点电势和电势梯度后，通过能量平衡法求解复介电常数的实部和虚部。

每个网格单元的静电储能可以表示为

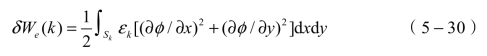
式中，εk、Sk分别表示第k个单元的介电常数和表面积。

云雾静电总能为

云雾的静电储能为

式中，εe为云雾等效复介电常数的实部；S为计算区域内复合材料的上（下）底面积；d为上下底之间的距离。

通过调整基本单元的边长，云雾粒子模型的浓度在95%～5%范围内变动，获得相应的云雾等效介电常数。各次仿真参数如表5-1所示，仿真计算如图5-7、图5-8所示。

表5-1　仿真计算参数表

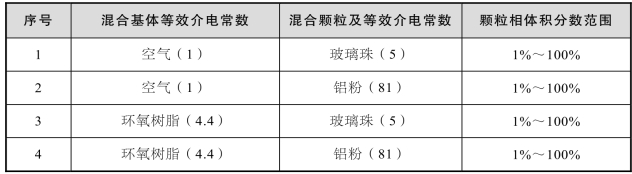
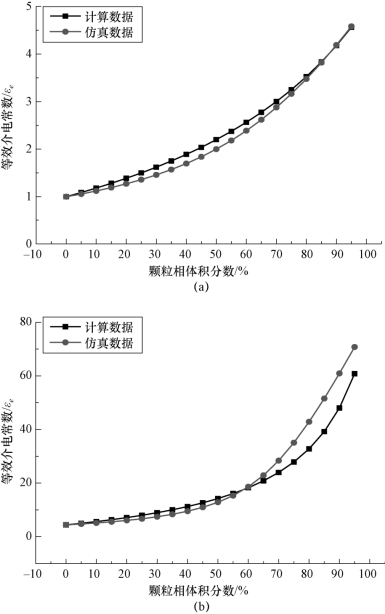
图5-7　空气—颗粒等效介电常数对比曲线

（a）空气—玻璃珠混合物；（b）空气—铝粉混合物

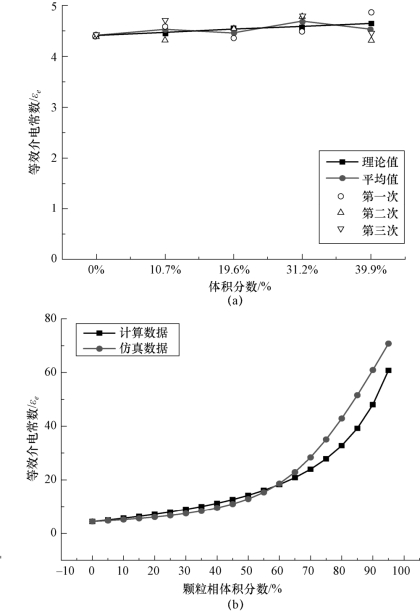
图5-8　环氧树脂—颗粒等效介电常数对比曲线

（a）环氧树脂—玻璃珠混合物；（b）环氧树脂—铝粉混合物

由上述数据对比可知，所述等效介电常数计算模型计算结果与仿真结果在低浓度段具有良好的一致性，且混合物成分介电常数越接近，计算结果一致性越好。