6.4.1 超声衰减仿真分析
采用流场仿真软件FLUENT对单个球形颗粒的声波衰减作用进行分析,获得声压作用下的声波衰减情况。仿真过程假定颗粒为刚性小球,仿真云图及颗粒圆周方向声压损失曲线如图6-4所示。
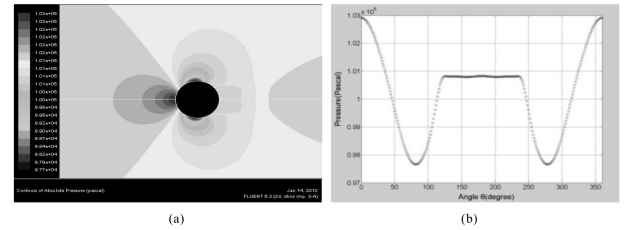
图6-4 单球形颗粒的声波衰减
(a)衰减云图:左侧为加压端,右侧为检测端;(b)声压损失曲线
同时,使用COMSOL多物理场耦合仿真软件对颗粒团簇的声衰减情况进行仿真分析。仿真模型采用COMSOL Multiphysics软件中的声学模块,该声学模型采用时谐声压模型,计算模型采用修改的亥姆霍兹方程,如下列方程所示:

式中,∇表示拉普拉斯算子;ρ表示介质密度;p表示声压;ω表示角频率;cs表示介质中的声速。介质的声阻抗和声速之间存在如下关系:
![]()
介质密度由如下方程定义:
![]()
式中,Zc表示复数阻抗;kc表示复波数。
对于声波能量衰减有如下方程表示:

式中,w0表示声波入射能量;wi表示声波出射能量。

使用COMSOL软件建立腔体状仿真模型如图6-5所示。
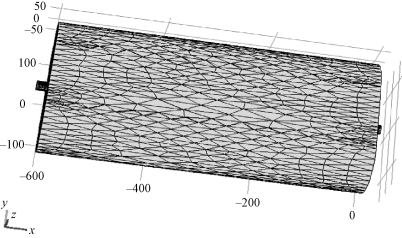
图6-5 超声腔体状仿真模型图
仿真模型中填充“空气—金属粉颗粒”混合物,采用蒙特卡洛法生成随机分布颗粒系,仿真过程如图6-6所示。

图6-6 整体模型的绝对声压云图
如图6-7所示,仿真过程中可以获得不同截面处的声压,采用面积积分方法获得接收端声压,除以接收面积获得接收端的平均声压,最终可以结合声源声压计算出该仿真条件下的声衰减系数。
选取“空气—金属粉颗粒”混合物为研究对象,设置体积浓度范围为1%~10%,浓度步进值为1%,分别采用计算机仿真计算和本书所述简化模型两种方法进行声波衰减计算。选取混合物浓度为横坐标,相应声衰减系数为纵坐标,可以获得三种方法的计算结果对比曲线,如图6-8所示。
由上述对比曲线可知:
(1)仿真结果与计算结果趋势一致,但是计算方法获得的衰减系数大于仿真结果,分析后认为是由于计算机仿真模型将混合物视为均匀介质,忽略了散射衰减损失引起的。
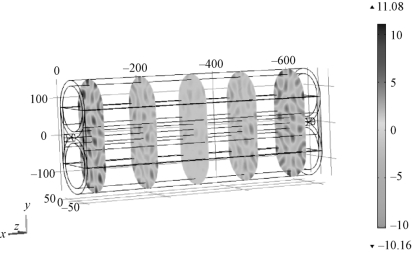
图6-7 不同截面的绝对声压云图
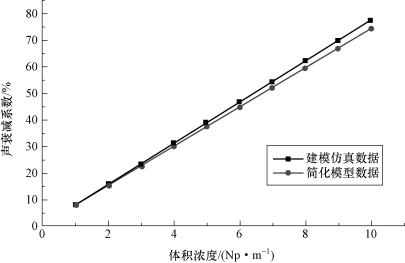
图6-8 两种模型仿真计算结果对比曲线
(2)对两种计算方法获得的结果进行对比分析发现,在低浓度段,两种模型的衰减系数相近;随着浓度增大,两种方法计算偏差开始增大。
