6.2.3 非理想黏性介质中的超声传播特性
在理想介质中,超声波受到超声传播距离、介质的黏滞系数、超声反射系数等多种因素影响,导致超声能量的衰减。但是传播过程是绝热的,不会与介质发生热交换。实际上超声波的传输衰减机理非常复杂,声波(尤其是高频声波/超声波)在传播过程中会与介质颗粒发生摩擦和热交换,并产生反射和多重反射等现象,很难对非理想介质中的声波衰减进行准确的理论分析,通常会根据实际的研究应用需求,针对主要的某一种或多种具体的衰减模式进行分析。
目前主要根据超声波衰减的原理及其与传播介质的关系将超声波衰减分为四种主要形式,如图6-1(a)所示:一是由于超声波波束扩散造成的扩散衰减,二是由于介质的黏滞作用造成的黏滞衰减,三是由于介质的其他原因使声能转化为热能引起的热传导衰减,四是由于非均匀介质中的固体颗粒对超声波的散射造成的散射衰减。第一类衰减是由声源的特性引起,受到传播距离影响,与传播介质特性无关;后三类的衰减与介质特性紧密相关。由于本书主要研究超声波与介质之间的关系,所以仅对后三类衰减开展研究。
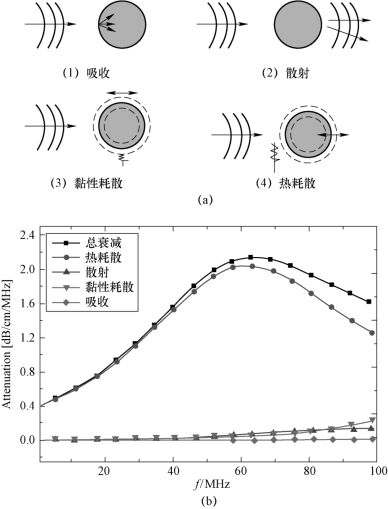
图6-1 声衰减机制示意图
(a)主要损失机制;(b)声衰减(体积浓度10%,尺寸0.16 μm)
6.2.3.1 黏滞衰减
当平面声波在非均匀介质中传播时,黏附于容器壁附近的介质点因受到很大的约束力,初速度很小,将其设为零;而离容器壁越远的介质质点受到的约束力越小,相应的速度也就越大,在介质中将会出现最大的速度值,因此声波在非均匀介质的传输过程中速度梯度将为弧度。由牛顿内摩擦定律可知,质点速度的差异,会在径向上形成不同的切应力,从而导致层与层之间的摩擦损耗,进而使超声波在非均匀介质中的信号衰减。

化简后得
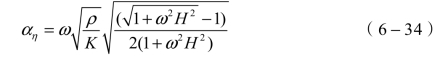
由于介质的黏滞力相对于弹性力很小,即ωH<<1,此时得到黏滞衰减系数的表达式为

由于ω=2πf,由式(6-35)可得

式中,η为介质的黏度,单位Pa.s;f为超声波的频率,单位Hz;ρ为非均匀介质的密度,单位kg/m3;c为声速,单位m/s。
超声波在非均匀介质中传输时,黏滞衰减系数αη与非均匀介质的黏度η、密度ρ、超声波的频率f有关,即在一定的非均匀介质体系中,超声波的频率越大,超声换能器接收到的信号幅值越弱,声黏滞系数越大;介质黏度越大,换能器接收到的信号幅值越小,声黏滞系数越大;介质的密度越大,换能器接收到的信号幅值越大,声黏滞系数越小。
6.2.3.2 热传导衰减
当超声波通过非均匀介质时,介质质点就会产生压缩、膨胀等变化。对于理想介质,由于介质的温度变化与体积变化是同步的,即当体积达到极小时温度就达到极大值,反之亦相同,此过程是可逆的,所以不存在热交换。但对于非均匀介质来说,由于声波过程是绝热的,且超声波的频率较大,其承载的能量也相对较大,因此当超声波通过非均匀介质时,介质受到超声波振动的影响,波动的热力损失将会出现,导致体积发生变化,压缩区域的体积将会变小,温度相应地升高;相反,温度会相应地降低。当相邻的压缩区与膨胀区之间存在温度梯度,高温区会向低温区传递一部分热量,发生热交换,即热传导。该交换过程将降低压缩区域的压力,使声波的振幅减小,整个过程是不可逆的。机械能转为热能的过程,引起超声波的衰减。
基尔霍夫导出介质的热传导引起的声衰减系数为

根据ω=2πf,可得

式中,χ为热传导系数,单位为W/m·℃;cv为介质的定容比热,单位为J/(kg·℃);cp为介质的定压比压,单位为J/(kg·℃);cv=cp/k,k为介质的定热比。
超声波在非均匀介质中传播时,热传导衰减系数αξ与介质的密度ρ、定容比热cv、定压比热cp和热传导系数χ以及声波的频率f有关,即在一定的介质中,超声波的频率越大,换能器接收到的信号幅值越弱,热传导衰减系数越大;同理,若介质密度越大,换能器接收的信号幅值越强,热传导衰减系数越小。
6.2.3.3 散射衰减
超声散射衰减本质上与光散射一样,指超声波在非均匀介质中传播时,介质的不均匀性造成微小的界面产生不同的声阻抗,导致声波向不同方向传播,引起声压或声能的减弱。当超声波通过非均匀介质时,介质中的固体颗粒使超声波发生了散射,改变了其传播方向,进而使其沿着相对复杂的路径传播下去;最终一部分声波传到了超声波换能器,换能器接收到回波信号,散射出去的超声波直接转变成热能,造成超声波的能量减少。散射衰减的过程不仅与介质的性质和状态有关,还与介质中固体颗粒的形状、尺寸大小和数目多少有关,在大颗粒和高频超声波条件下产生的作用尤为显著。在实际的理论研究中,通常会做比较粗略的估算,即把这些粒子当作完全刚性的、半径为r的球形物体。若单位体积中含有n个散射粒子,由瑞利理论可得散射衰减系数αs为

式中,k为超声波波数,k=2π/λ,λ=c/f 所以k=2πf/c;n为单位体积内粒子数目,n=3/2πr3,可得

超声波在非均匀介质中传播时,散射系数αs与介质中颗粒的尺寸大小r和声波的频率f有关,其大小与尺寸的三次方成正比、与频率的四次方成正比。即在一定的介质体系中,超声波的频率越大,换能器接收到的信号越弱,声散射衰减系数越大;同理,若介质中颗粒尺寸越大,换能器接收到的信号幅值越小,声散射衰减系数越大。
进一步,黏滞衰减、热传导衰减和散射衰减可以用指数方程统一表示:
![]()
式中,U0为超声波的初始幅值,U为超声波的接收端幅值;L为超声波在非均匀介质中传播的距离;α为总衰减系数,是黏滞衰减系数αη、热传导衰减系数αξ、散射衰减系数αs之和,即
![]()
声学量常用其比值的对数表示,一是因为声压、声强等的变化范围较大,通常能够达到十几个数量级,使用对数标度要比绝对标度更加方便;二是由于这些声学量用对数关系来表示时,超声波的声能数量级变化会更加明显,因此超声波在介质中的衰减更适合用对数表示。式(6-42)整理后得

实际测量中,U0和L为已知量,超声衰减系数α与接收端的超声波幅值U成对数关系,因此可通过U的变化研究介质参数对超声波衰减系数的影响。
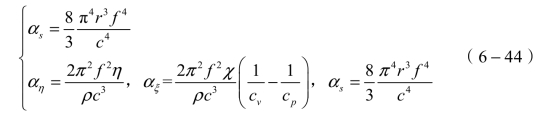
可知,超声波在非均匀介质中传播时,总衰减系数与介质中颗粒的尺寸大小、介质的黏度、介质的密度和声波的频率等有关。
对于成分已知的混合物,其等效密度为各成分密度与其体积分数的函数,如果测得超声波在该混合物中的衰减系数,则可以反解获得某一成分的体积分数,即可获得该混合物的浓度信息。
