2.2.4　燃料抛撒浓度分布模型

2.2.4　燃料抛撒浓度分布模型

2.2.4.1　坐标系建立

假设云雾区域概化为扁平的圆柱体，所使用的方法是将整个圆柱状云雾沿径向分割出单位弧度的一个长方体，按照轴对称原则，计算出长方体的浓度分布，如图2-7所示，网格点H（i，j，k）的坐标为（xi，yj，zk）。

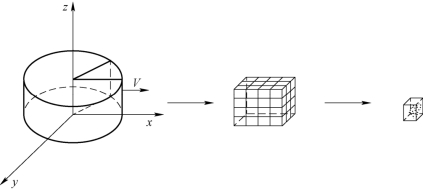
图2-7　云雾矩阵网络划分

利用笛卡儿矩形网格对长方体V中的颗粒坐标进行离散，得到各个颗粒或液滴离散化以后的坐标。

根据长方体V中颗粒或液滴的坐标值分布范围选择把长方体V划分成m×n×l个网格（图2-8）；计算得到网格的步长，即小格子ΔV的长宽高，如下式所示：

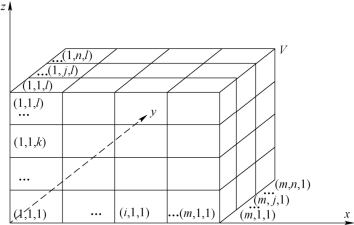
图2-8　长方体V三维矩阵（m×n×l）浓度分布

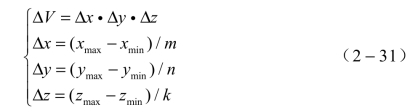
利用高斯函数，即取整函数y=[x]。对计算的结果取整数，得到颗粒的新坐标，如式（2-32）。新坐标点为（i，j，k）。其与原坐标点的关系如式（2-33）所示。

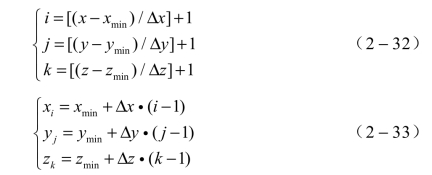
式中，x表示云雾区域中液滴或颗粒的径向距离，即长；y表示云雾区域中液滴或颗粒的高度；z表示云雾区域中液滴或颗粒的宽度距离。

2.2.4.2　浓度分布描述

对于颗粒的运动形成云雾过程，每个网格即小矩形盒子里的颗粒数量与颗粒质量均随时间发生动态变化。计算小矩形盒子在每个时刻的颗粒总质量，如下式所示：

式中，mq代表小矩形（ΔV）中颗粒在t时刻的质量（q=1，2，…，N）；t代表时间。假设这个网格（小矩形盒子ΔV）足够小，浓度可视为该网格，即该点（xi，yj，zk）处的浓度。

将所有小矩形盒内颗粒的总质量按其空间分布位置进行排列组合，可以得到整个区域的浓度分布。引入三维矩阵，如式（2-35）。其中aijk表示三维矩阵的第i行、第j列、第k页元素。

定义三维矩阵A的第i行、第j列、第k页的元素为1，其余元素均为0，如式（2-35）所示。如果A=A1：A2：…：Al，则三维矩阵A（m×n×l）可以反映出图2-8中矩阵中各元素的位置分布。变换矩阵A用于将计算得到的单个网格点（小矩形盒子）的浓度值映射到整个区域的浓度矩阵中，并确定其在区域中的位置。

因此，燃料颗粒或液滴浓度分布为网格点处存在的颗粒质量分布的叠加，进一步为各小矩形盒颗粒质量分布的叠加。

2.2.4.3　浓度分布计算

设表示第t时刻小矩形框ΔV（i，j，k）的凝聚相浓度，表示第t 时刻小矩形框（i，j，k）的凝聚相浓度矩阵，C（t）表示第t时刻整个区域的凝聚相浓度矩阵，可以计算为

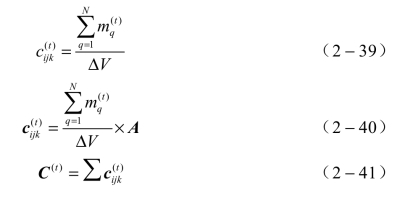
假定液滴由于蒸发效应和剥离效应质量减小。除蒸发效应产生气体外，由于液滴高速运动，跟周围空气的速度差引起液滴表面的气动摩擦，因此，由剥离效应产生的小液滴也转化为气体。因此可以假定颗粒减少的质量全部转化为气体，即颗粒在两个时刻（t，t+Δt）的质量差就是（t+Δt）时刻生成气体的质量。

2.2.4.4　权函数加权平均算法

为了更好地研究离散数据所表示的原来模型，首先要把离散数据向连续方面过渡，就是通过这些数据点，去拟合一个光滑的空间曲面z=f（x，y）。网格化处理的常用方法有Taylor级数三点展开法、有限元插值法、逐步订正法、反距离加权平均法、径向基本函数法等。因为抛撒颗粒的分布是散点形式，并且空间位置的数据已知，所以选择反距离加权平均法进行曲面拟合。反距离加权法最早由Richard提出，并逐渐在各个领域得到发展，各样本对插值结果的影响随距离的增加而减小。反距离加权法的优点是逐步比较找出距离格点不同距离的点，根据距离远近分别给予不同的权重系数。

根据已知的数据点集（xi，yi，zi）（i=1，2，3，…，N），其中xi，yi，zi分别表示液滴或颗粒在圆柱形云雾中的径向距离、高度及所在区域的浓度，液滴或颗粒数目为N，通过构造一个全部数据点都满足的光滑曲面Z=F（X，Y）。先将点（xi，yi，zi）投影到XY平面上，任一点（xi，yi，zi）的投影为D（xi，yi），该点高度值为zi，则在XY平面上的任一点P（x，y）高度值z，是受到所有（xi，yi）的高度值zi对该点影响的结果。这种影响的大小与点P（x，y）到其他点之间的距离有关，距P点远的点的zi值对P点影响小一点，距离P点近的点的zi值对P点影响大一点。把距离作为权，所有点（xi，yi）对P点Z值的影响进行加权平均就得到了P点的Z值，即各数据点的Z值按与P点的距离加权平均，距离小的所加的权大，距离大的所加的权则小。

曲面拟合公式：令Zi是D（x，y）点的Z值，d（P，Di）为P（x，y）与D（xi，yi）之间的距离，在P（x，y）认定时，可简记为di。当P（x，y）在D（x，y）的邻域时，的性质类似于或（di）u-1。因此，对于u＞1，当P→Di时，依（x-xi）（或di）趋于零，对于u=1，左右偏导数都存在，一般它们是非零的，而且符号相反；对于u＜1，偏导数不存在。因此，曲面光滑性要求u＞1。

根据上述，P（x，y）点的Z值可以表示为

根据计算的点数由全部数据点减为P（x，y）附近点，半径r以外的数据点的贡献由半径r以内的数据点进行补偿，这些数据点集合为C′，并使得整个曲面处处连续可微。为此，权函数改为如下定义：

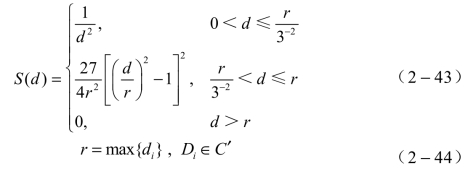
考虑不同方向数据点的影响不同，所以进行方向加权，即对于每个Di（x，y），同时要考虑其他各Dj（x，y）点相对Di（x，y）点的分布，可以通过DjP在DiP上的投影来度量，因此，引入与夹角的余弦cos（DjPDi）作为分布的一种测量。

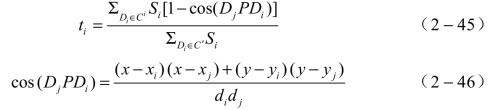
因此，当同时考虑距离和方向因素时，需要引入一个新的权函数：

为了使所构造的曲面具有所估计的偏导数，对每一个属于C′的点Di（x，y），必须计算一个作为P（x，y）点的数的增量ΔZ，将此增量加到曲面上，曲面在Di（x，y）点上存在期望的偏导数。这个ΔZ可取为

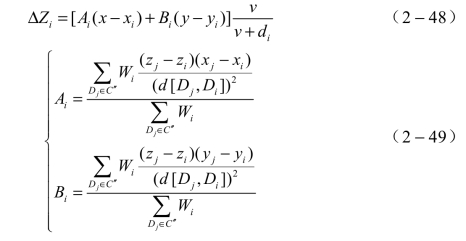
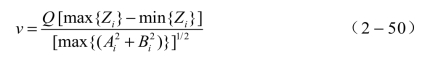
当P（x，y）点很接近某个点Di（x，y）时，舍入误差和截断将引起很大误差，另外计算机计算时也会有很大困难，如算术溢出等。这些问题可以通过在Di（x，y）上建立一个邻域加以避免，一旦点P（x，y）落进这个邻域，则令f（P）=Z。

如果P（x，y）同时落入几个Di（x，y）的邻域内，则取它们的Z值的平均值作为P（x，y）点的Z值。把这几个Di（x，y）组成的集合定义为N（P），则此时云雾抛撒浓度分布曲面函数如下式所示：

式中，Wi为权函数；C′为参加运算的点的集合；C″为C中P（X，Y）的ε邻域中Di的集合。