8.4.2　 卡尔曼滤波融合的底层数据融合

8.4.2　 卡尔曼滤波融合的底层数据融合

卡尔曼滤波的数学实质在于采用预测方程和测量方程寻找在最小均方误差XK下的估计值XK。假设动态系统的状态方程和测量方程分别为

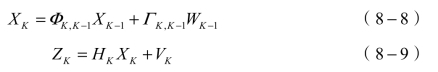
式中，XK是K时刻的系统状态；ΦK，K-1和ΓK，K-1是k-1时刻到K时刻的状态转移矩阵；ZK是K时刻的测量值；HK是测量系统的参数；WK和VK分别表示过程和测量的噪声，假设为高斯白噪声。如果被估计状态和观测量满足式（8-8），系统过程噪声和观测噪声满足式（8-9）的假设，K时刻的观测XK的估计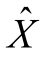可按下述方程求解：

状态估计：

滤波增益矩阵：

进一步预测误差方差阵：

估计误差方差阵：

在给定初值X1和P0的条件下，根据K时刻的观测值ZK，可以递推计算得K时刻的状态估计XK（K=1，2，…，N）。

对采集的双频超声浓度特征数据进行滤波处理，如图8-8所示。原始浓度信号数据波动剧烈，显示出较大的噪声值，经过卡尔曼滤波处理之后，数据明显变得清晰平滑，噪声得到了有效抑制，同时又完整保留了所有有效数据的特征值，有效提高了数据精度，降低了干扰噪声，为后续处理提供更为可信的浓度信息。

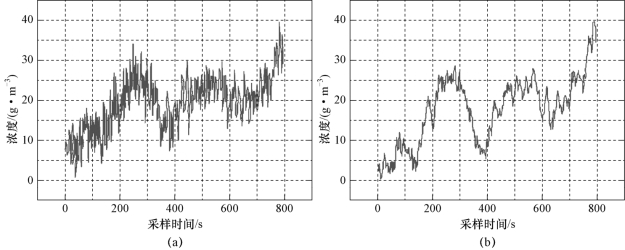
图8-8　滤波效果对比曲线

（a）滤波前；（b）滤波后