5.2.3 基于Clausius-Mossotti理论云雾浓度计算模型
5.2.3.1 介电常数计算
电介质的介电常数是表征电介质电性能的宏观参数,它是电介质足够大区域内的平均值,概括了物质的所有介电和光学特性。材料的介电常数与组成它的分子的电极化性质有关。
一般地,物质分子局部电场Eloc作用而产生电偶极矩p。强电场情况下,应将p展开成电场强度Eloc的泰勒级数,若电场不太强,可忽略非线性项,取该展开式的一次项近似,即为:
![]()
根据介质极化强度定义有:
![]()
式中,n为电介质的单位体积分子数。电场Eloc为作用于极化分子的局部电场,这个场是由外加电场E与介质中所有其他分子电偶极矩产生的电场E′叠加形成的,即有:
![]()
H.A.Lorentz采用均匀介质中的球形空腔模型,计算出球腔内壁电荷密度-Pcosθ在球心处产生的电场E′为:

即有:
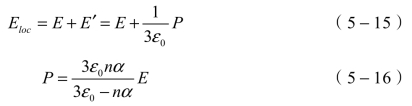
根据电介质宏观极化率的定义有:
![]()
因此有:
![]()
根据电磁学中电介质相对介电常数的定义有混合物的等效介电常数ε为:
![]()
最终可得

上式即为Clausius-Mossotti公式。该公式揭示了电介质极化现象中的微观特性单位分子数n、分子极化率α和电介质宏观参数介电常数ε之间的关系,为建立混合物等效介电常数奠定了基础。
5.2.3.2 云雾粒子浓度计算
对于由两种成分构成的混合云雾,对云雾和两种成分分别应用基于空气混合极化的Clausius-Mossotti公式有
对于云雾
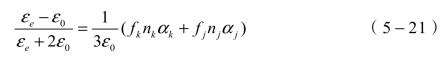
对于颗粒物

对于基体

式中,εe为混合物的等效介电常数,ε0为空气的等效介电常数,εj为成分2的介电常数,εk为成分1的介电常数;αk为成分1的分子极化率, αj为成分2的分子极化率,且有fk=nk/(nk+nj),fj=nj/(nk+nj)。
联立以上三式,并代入fk和fj的关系,可得
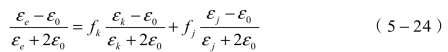
假设混合物中两种成分的体积分数相差较大,可以等效为少量颗粒弥散于介质基体中,颗粒间距较大,颗粒间相互作用可以忽略不计,混合物结构可以表示为图5-4的形式。
此时,对混合物浓度计算模型进行修正,采用混合物颗粒成分体积分数φ代替分子比例fk,采用基体相关介电参数代替空气介电常数,即εj=ε0,则有
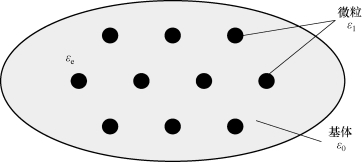
图5-4 云雾粒子结构简图

上式即为颗粒云雾浓度(体积浓度)的计算模型。
