8.4.3 基于测量误差差值的自适应加权算法的顶层数据融合
8.4.3.1 常规最优加权数据融合算法
最优加权数据融合算法原理:设{yt},L=1,2,…,n为观测值序列,对未来L个时刻值y(n+L),L=1,2,…,k,用I种模型获得预测值![]() ,i=1,2,…,I;再根据对各单一预测模型预测结果的分析,确定各单一预测模型在组合预测模型中的最优权重wi(i=1,2,…,L),这样就构成了组合预测模型:
,i=1,2,…,I;再根据对各单一预测模型预测结果的分析,确定各单一预测模型在组合预测模型中的最优权重wi(i=1,2,…,L),这样就构成了组合预测模型:

式中,yn+L为未来L期的预测值;yn+L(i)为用第i种模型预测的未来L期的预测值;wi为第i种模型的权重且![]() 。
。
基于上述模型原理,假设每套多模复合浓度检测系统中包含m套声学测试装置,待测云雾瞬时浓度估计值为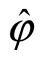 ,高频超声测量结果为φsi,低频超声测量结果为φej,高频测量值和低频测量值的权重分别为wsi和wej,高频测量值和低频测量值的方差分别为σi和σj。则以上数据满足以下基本关系:
,高频超声测量结果为φsi,低频超声测量结果为φej,高频测量值和低频测量值的权重分别为wsi和wej,高频测量值和低频测量值的方差分别为σi和σj。则以上数据满足以下基本关系:
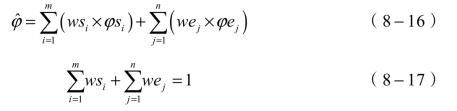
总体方差为
![]()
当且仅当测量权重满足下式时可以获得最小总体方差:
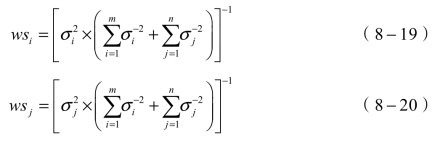
获得的最小总体方差弹可表示为
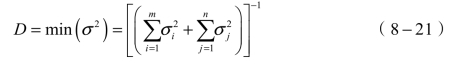
则浓度估计值可以进一步表示为
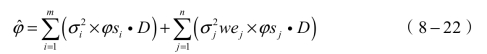
且可知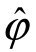 服从正态分布,即有
服从正态分布,即有
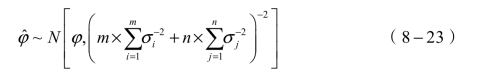
8.4.3.2 基于测量误差差值的自适应加权数据融合算法
最优加权数据融合算法的理论精度由其样本数量决定,采用无限时间窗时,即具有全部的历史数据。该方法在理论上能够获得最小的总体方差D的数据融合结果。但是在实际应用中该算法的应用受到较多限制,例如对于计算实时性要求较高的系统和动态性较高的系统,最优加权数据融合算法并不适用,因此研究人员在上述算法的基础上又提出了多种自适应加权算法,将各权重wsi变成为某些特征数据ε的函数,即wsi=Φ(ε),且保证
![]()
通过采用自适应加权数据融合算法,可以有效地提高加权算法在动态系统和实时性要求较高的系统中进行数据融合的作用效果,因此极大地推进了加权数据融合算法的应用。不同的研究人员根据各自不同的研究需求,提出了多种有效的权重自适应函数,极大地丰富了加权数据融合算法的应用领域。
由前所述可知,本研究应用的测量装置(超声探测系统)是典型的同质非恒定误差传感器测量设备,即高频和低频测量系统的系统误差eH 和eL均为时变值。其变化规律为:在云雾抛撒作用过程中,eH 和eL伴随粒径和浓度不断变化,在抛撒初期(粒径大,浓度高)阶段低频超声测量误差小于高频超声测量误差,在抛撒中后期(粒径小,浓度低)高频超声的测量精度明显高于低频超声的测量精度,如图8-9所示。
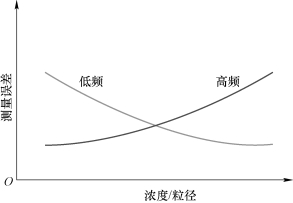
图8-9 高/低频声波测量误差趋势图
根据上述特性,提出了一种基于测量误差差值的权重自适应变化算法:采用若干组历史数据获得一个窄时间窗内的浓度均值作为前一时刻的浓度值,即有
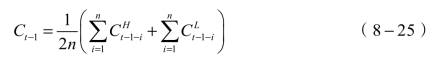
采用该浓度值计算本次测量的两个误差:

再如上获得t+1时刻的测量误差![]() 和
和![]() ,则可以获得两个误差的差值绝对值:
,则可以获得两个误差的差值绝对值:

然后对![]() 和
和![]() 的大小和数值,分段使用Tanh函数进行权重计算,Tanh函数方程如下:
的大小和数值,分段使用Tanh函数进行权重计算,Tanh函数方程如下:

如图8-10所示,Tanh函数是双曲正切函数,返回以弧度为单位的x为输入参数的双曲正切值,其图像被限制在两水平渐近线y=1和y=-1之间。Tanh函数作用于数组中的每一个元素,这个函数的域和范围包括幅值,并且所有的角度都以弧度的形式表示。
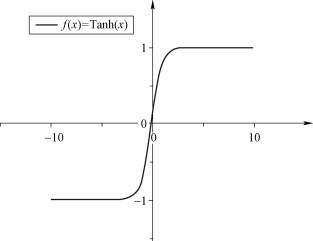
图8-10 Tanh函数
当![]() ,即高频超声误差和误差差值较大时,有
,即高频超声误差和误差差值较大时,有
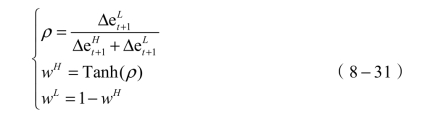
当![]() ,即低频超声误差和误差差值较大时,有
,即低频超声误差和误差差值较大时,有
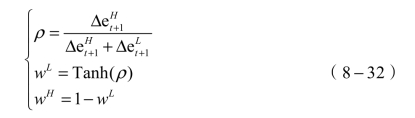
当![]() 时,取wL=wH=0.5。
时,取wL=wH=0.5。
然后采用上述权重计算方式,代入加权数据融合算法中进行加权数据融合,即可获得融合结果。取历史数据计算深度为8,对上述数据融合算法进行仿真计算,计算结果如图8-11、图8-12所示。
由上述仿真结果可知,采用高频超声检测获得的数据与标准设备相比,检测误差越来越小;低频超声检测获得的数据与标准设备相比,检测误差越来越
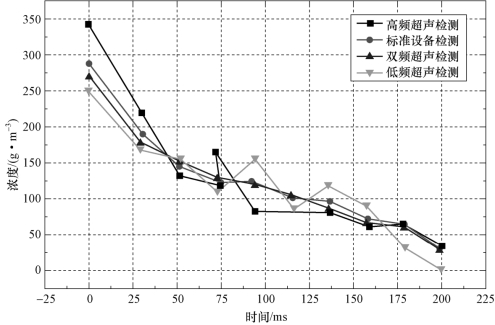
图8-11 数据融合算法效果测试(彩图见附录)
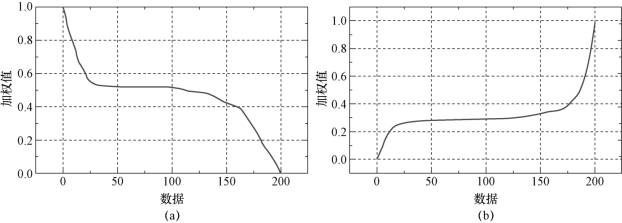
图8-12 高频/低频超声数据的权重曲线
(a)高频;(b)低频
大;双频超声检测获得的数据与标准设备比较接近。由此可以得出高频超声和低频超声在高浓度段和低浓度段各自都有自己的检测优势和缺点,只有采用两者检测的数据进行融合后才能获得良好的效果。采用基于测量误差差值的自适应加权数据融合算法可以获得更加贴近真实值的计算结果。
进一步调整计算深度,得到不同深度下的总体测量误差,如表8-2所示。
表8-2 不同深度下的总体测量误差

