6.2.1 理想粒子介质中的超声传播特性
超声波在介质中的传输过程中，可以认为相位和振幅保持不变以及能量守恒，因此对超声波在介质中传播的基本特性进行理想化假设：
（1）介质是非黏性的，即超声波在介质中传输时没有能量损失。
（2）介质是相对静止且均匀的，即初速度为零，静态压强和静态密度是常数。
（3）超声波传输过程是绝热的，即传输过程中没有温度差引起的热交换，即介质的相邻部分不会因为温度差进而产生热交换。
（4）在介质中传输的是小振幅超声波，即各声学的变化量都是很小的量。
根据上述假设，对声场进行分析如下：
1.连续性方程
设声场中单位体积元Δv，根据质量守恒定律，单位体积内流入体积元的质量与流出的质量之差即该体积元内质量的变化量，由此得到声波的连续性方程：
式中，ρv表示流量密度；x表示传播距离；p表示声压；t表示作用时间，可得流量密度在某处的散度负值和介质中压强在该点的时间变化率相等。
2.物态方程
假设超声在无扰动条件下传输，颗粒介质设定为一定质量、一定体积的单元，其状态用声压p、密度ρ和热力学温度T表示。当超声波传输至该体积元时，其体积将会产生压缩与伸张形变，导致介质中的参量状态将发生变化，即p、ρ、T会发生相应的变化。由于p、ρ、T三者之间的变化存在内在联系，因此建立描述状态变化过程的数学模型，即可表征超声波作用下介质密度和声压参量之间的变化关系。
根据热力学理论可知，对一定质量的介质来说，其状态方程可用p、ρ及系统熵s三者之间的关系来表示。在等熵情况下，密度增量dρ和相应的压强增量dp之间的关系为一比例常数，比例常数可用c2表示，由此得到声波的物态方程：
上述假设中各声学的变量都是微量级，因此它们的平方项可忽略不计。根据拉格朗日公式，其超声波传播的物态方程可近似为
此物态方程表征介质状态中压强和密度之间的线性关系。
3.运动方程
超声波在连续的介质中传播时，由于各处的受力情况不同，因此压强也不一样。假设在超声场中取一足够小的体积元Δv，超声波的振动使其体积元在x轴方向受到的作用力大小不等，由牛顿第二定律知道，声波运动方程为
运动方程反映出声场中声压p与质点速度v两者之间的相互关系，ρ为密度。
4.波动方程
根据上述分析，得出超声场的连续方程、物态方程和运动方程。三个方程之间相互独立，消去p、ρ、v中任意两个参量，就可得到另一个变量。由于声速v是矢量，密度的变化量ρ不易测量，因此超声学理论分析和测量中常用声压p描述声场。理想介质中关于声压p的波动方程为
波动方程反映了p、t和空间x之间的关系，这种时空变化的关联，反映了波动的性质。对x和t求导得到关于速度v的波动方程：
质点速度表示为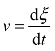
，代入式（6-6），得到质点位移的波动方程：
超声波在理想介质中仅考虑在一维方向上传输，认为其他方向上质点的振幅和相位是不变的，即超声平面波。平面声波的波阵面是平面，因此将任一平面超声波都近似认为其具有相同的特性。
考虑在简谐声源作用下，声场随时间的变化中产生稳态声场。由傅里叶变换分析时间函数在不同频率的简谐函数的变换，因此波动方程的解有如下形式：
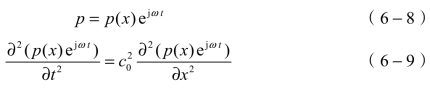
化简可得
设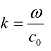
（k为波数），p是关于x的函数，即有
取成复数解形式：
其中，C、D为任意的常数，由边界条件决定，进一步得到
其中，第二项表示反射波，我们讨论的是超声波无限介质中的传输问题，因此不考虑其反射波，即D=0，化简后为
当C取值边界条件x=0时，即在声源处振动时，相邻介质产生的声压为
理想状态下关于声压p的一维波动方程的解为
即在沿声波传输方向，超声声压随传播距离产生指数衰减。