6.2.2　理想黏性介质中的超声传播特性

6.2.2　理想黏性介质中的超声传播特性

声波传输中的介质往往都是非单一成分的黏性介质，不但有固相物质的存在，还存在气泡、固体颗粒、杂质等，往往显现出黏性等特征，产生不同形式的能量衰减，因此超声波信号在黏性介质中的传输需要考虑的物理参数存在不确定性，比理想状态下模型更为复杂。

黏性介质在实际情况下虽然存在一定的初速度，但远远小于超声波在介质中的传输速度，因此介质的初速度可以忽略不计。简化方程的推导，对理想黏性介质做如下假设：

（1）介质为黏性流体，动力黏度为η；

（2）介质是静止的，初速度为零；

（3）介质是均质的，密度为ρ；

（4）介质中不存在温度差引起的热交换，即为绝热过程；

（5）超声波为小振幅声波，即各声学变量是一阶为分量。

由介质的绝热体积弹性系数定义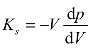，得到

Δ为有超声扰动时，引起的体积相对变化量，对于平面波有

用声压p表示压强增量Δp，得到

根据非均匀介质中相邻质点的运动速度不相同的条件，它们之间会因内摩擦力的作用而产生相对运动。有牛顿定律可知，单位面积上介质的黏滞力为

压强的增量可表示为

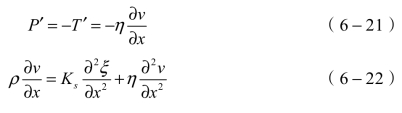
由于质点速度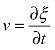，代入上式，得到超声波关于位移ξ的非理想介质中波动方程：

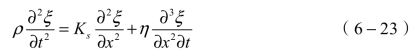
对于简谐声波，设波动方程的解为ξ（x，t）=ξ1（x）ejωt，得到

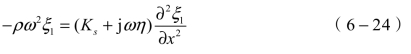
令K=Ks+jωη，有

令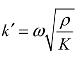，则上式化为

对比理想状态下波动方程的解，得到非均匀介质的波动方程的解为

由于上述中k是复数形式，所以k′也是复数形式，令（αη为黏性介质的系数），代入上式得

上式第一项表示传输速度为c，角频率为ω的入射波，第二项表示向负方向传输的反射波。

忽略反射波的影响，即有

则超声波在非均匀介质中传输的波动方程的解为

如果声源在x=0处振动，上式化为

对比两类超声传播特性可知，当介质发生变化时，声波的传输特性发生了明显的变化，这种变化与αη等介质特性密切相关，即超声波的传输特性包含了传输介质的相关特性。