11.3.1 人工神经网络(ANN)
人工神经网络(ANN)是通过训练网络来表示数据内在的关系或过程来开发ANN模型。它们实质上是非线性回归模型,使用一组互连的节点或神经元执行输入/输出映射。每个神经元从外部或从其他神经元接收输入,并通过激活或传递功能将其传递。
通常,ANN具有三种拓扑:多层,单层和递归。多层ANN通常由一个输入层、一个或多个隐藏层和一个输出层组成。对于单层ANN,没有隐藏层。循环ANN至少在网络中包括一个反馈回路。对ANN进行分类的另一种方法取决于学习策略:有监督或无监督。在监督学习中,训练数据集既包含输入对象又包含所需的输出,在非监督学习中,数据未标记。已经开发了多种ANN模型并将其进行了一系列应用,例如:模式识别,关联存储器,优化,函数逼近,建模和控制,图像处理和分类。
其中,MLP算法和RBF神经网络已应用于多相流量测量,本节将对这两种ANN进行简要介绍。
11.3.1.1 MLP算法
图11-2描绘了典型的m输入一层/输出三层ANN的结构。
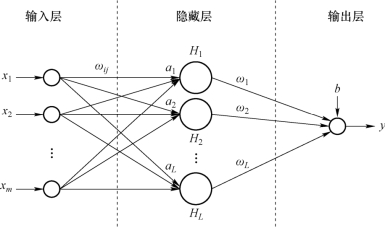
图11-2 输入一层/输出三层ANN的结构
x=(x1,x2,…,xm),T是输入样本,y是所需的输出。假设y是隐藏神经元的线性输出,转移函数f(x)用于神经元,其ANN建模为
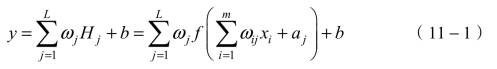
式中,m和L分别是输入变量和隐藏节点的数量;ωj是连接第j个隐藏节点和输出节点的权重;ωij是将第i个输入节点连接到第j个隐藏节点的权重;aj和b分别是第j个隐藏节点和输出节点上的偏置。层之间的权重(ωij和ωj)和偏差(aj和b)是通过训练过程获得的。
神经网络的性能取决于其结构和学习算法的选择。ANN结构的设计考虑因素包括输入、输出、隐藏层和隐藏神经元的数量。网络输入可以是对于预测输出很重要的变量的任何组合。因此,有关该问题的一些知识以及输入变量选择的过程非常重要。隐藏层的数量是根据问题的复杂性确定的。通常,问题越复杂,就需要越多的隐藏层来达到良好的近似水平;同时,近似水平和计算成本之间应该折中。可以使用一些准则确定隐藏层中神经元的数量(L),例如:

式中,m和n分别是输入变量和训练样本的数量。但是,这些规则仅给出了L的范围,应通过反复试验来选择模型的确切L,以在最小化误差和获得良好的泛化能力之间进行折中,输出层中节点的数量等于所需输出变量的数量。
层之间的传递函数可以是S型、双曲正切S型、线性、高斯和指数等,这取决于网络的性能。反向传播(BP)算法是训练过程中最流行、功能最强大的工具之一。它是梯度下降优化算法的一种变体,在每个训练周期之后调整神经元之间的权重,可以最大限度地减少预测输出值和实际输出值之间的误差。
11.3.1.2 RBF算法
如图11-3所示,RBF-ANN具有固定的三层结构,并将一种径向基函数作为激活函数应用于隐藏节点。网络的输出是输入的径向基函数和神经元参数的线性组合。径向基函数测量输入矢量和权重矢量之间的距离,通常认为是高斯函数。网络的输出由文献[16]给出,即
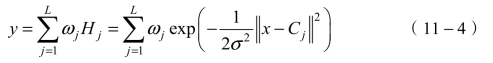
式中,Cj是第j个隐藏节点的中心向量,并由K-means聚类方法确定;![]() 是欧几里得范数,σ2是高斯函数的方差。
是欧几里得范数,σ2是高斯函数的方差。
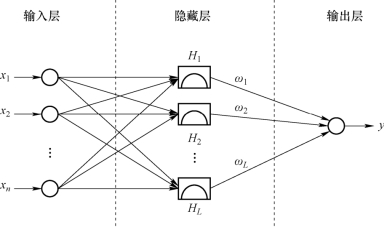
图11-3 RBF-ANN的结构
具有足够隐藏节点的RBF网络可以任意精度近似任何连续函数。此外,作为局部近似网络,RBF神经网络具有结构简单、形容词参数少和训练有效的优点。
