11.3.2 支持向量机（SVM）
SVM由Vapnik于1995年开发，旨在基于统计学习理论和结构风险最小化来解决分类问题，该方法已扩展到回归和预测问题，如图11-4所示。SVM通过非线性映射ϕ（x）将数据x从输入空间映射到特征空间，约束优化方法用于识别和分类。
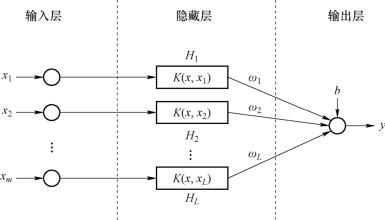
图11-4 SVM结构原理图
11.3.2.1 SVM作为分类器
给定n个训练样本X*=（x1，x2，…，xn），并且相应的期望输出Y=（y1，y2，…，yn），每个输入样本都是向量x=（x1，x2，…，xm），T由m个变量组成。使用传递函数ϕ（x）将输入向量映射到L维特征空间。特征空间中两个不同类之间的距离为
。为了最大限度地提高分离余量，使训练误差最小化ξi等于
。
式中，ξi是松弛变量，C是指定的参数，并且在分隔边距的距离与训练误差之间进行权衡。
基于Karush-Kuhn-Tucker（KKT）定理，该问题等效于以下双重问题：
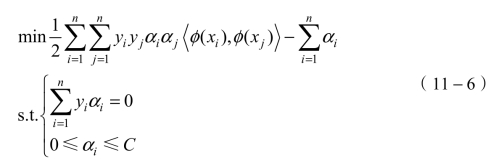
其中，每个拉格朗日乘数αi对应于训练样本（xi，yi），
是核函数。SVM分类器的决策功能描述为：
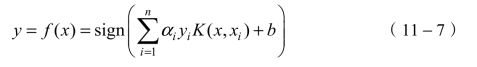
SVM有一些可选的内核功能，例如：
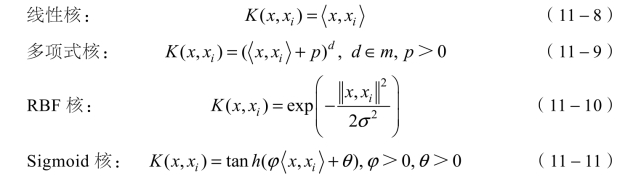
11.3.2.2 SVM作为识别器
SVM回归使用ε不敏感损失在高维特征空间中执行线性回归，并且倾向于通过最小化
来降低模型复杂度。通过引入松弛变量ξi和
（i=1，2，…，n）来测量ε不敏感区域之外的训练样本（X*，Y）的偏差来描述。通过最小化训练数据的经验风险来获得回归估计，因此，将优化问题表述为
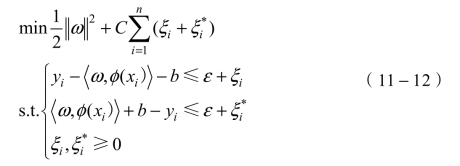
式中，n是训练样本的数量，ε是在不可行情况下可以通过松弛变量ξ和ξ*的近似精度。C是一个正常数，作为正则化参数，可以调整函数f（x）的平坦度和大于ε的偏差公差之间的折中。通过KKT条件来计算参数b。
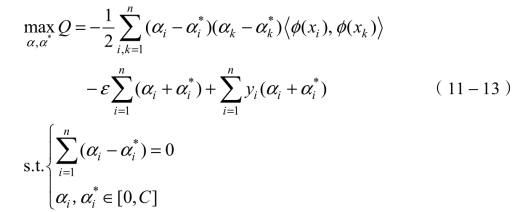
根据Mercer的条件，可以通过内核K（x，xi）定义内积
，因此SVM方法中训练过程的最终乘积可以表示为
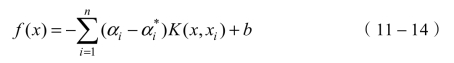
支持向量机是带有相关学习算法的监督学习模型，可以对数据进行分类和回归分析。原始公式带有一组标记的数据实例，SVM训练算法旨在找到一种超平面，该超平面以与训练示例一致的方式将数据集分为离散的预定义数量的类。近年来，已经开发了一些支持向量机的优化模型，例如最小二乘支持向量机、孪生支持向量机、多内核支持向量机和模糊支持向量机，以提高计算效率和泛化能力。