10.5.1 基于缩比动态云雾的浓度检测试验
基于缩比模拟抛撒装置的动态燃料云雾浓度检测试验主要使用广域动态云雾浓度等效检测模型,采用缩比抛撒装置,模拟云爆弹燃料抛撒过程;通过爆炸抛撒方式产生小范围的动态燃料云雾,对浓度测试方法和系统的检测精度进行评估验证。
燃料抛撒云雾形状受到弹体结构、壳体材料、长径比和比药量等因素影响,实际抛撒过程中还受到环境气象条件作用,云雾形状极不规则。现有云爆弹燃料抛撒分析研究中,常用简化体积模型,如圆柱体或椭球体计算模型,从而引入较大的模型误差。本研究提出采用外轮廓线旋转积分方法计算云雾体积,如图10-23所示。由于常规云爆弹均为轴对称结构(圆柱状),可以假设云雾形状以过爆炸中心的铅垂线对称;通过图像分析方法计算云雾体的几何中心,同时检测不同高度处云雾直径,根据旋转体积积分公式,沿高度积分即可计算出云雾体积。其具体实现过程如下:
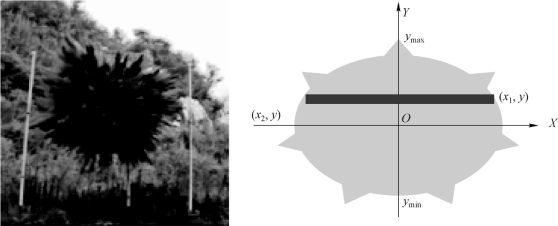
图10-23 基于旋转体积分方法的体积计算模型
如图10-23所示,点O为采用图像处理方法获得的云雾中心,过该点设置正交坐标系,设在Y轴某处取一厚度为dy,直径为D=x1-x2的薄片,且认为该薄片沿Y轴中心对称,则该薄片的体积dV为:

对上式沿Y轴积分可得云雾体积为
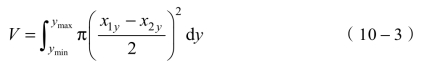
根据高速摄像机对云雾尺寸进行精确检测,云雾变化过程如图10-24所示。通过上述的旋转体积法进行云雾尺寸的计算,得到云团尺寸—时间曲线(图10-25)、云团体积—时间曲线(图10-26)。通过获得的云团尺寸,进而实现对云团浓度进行计算,如图10-27所示。
其中,x1y、x2y为不同高度处云雾尺寸。
对于不同高度处云雾尺寸的检测误差是影响精度的关键因素,为了尽量减小该误差,在实际检测云雾尺寸时,可以根据云雾图像特征选取不同的云层厚度dy;同时,使用多台高速摄像机进行不同角度拍摄时,可能获得同一云雾不同视角下的不同直径,此时可以采用求均值方法按照圆柱形计算旋转体半径:
![]()

图10-24 抛撒过程的高速摄像图片
(a)t=2ms;(b)t=4ms;(c)t=6ms;(d)t=8ms;(e)t=10ms;(f)t=20ms;(g)t=30ms;(h)t=40ms
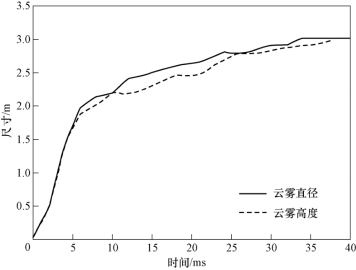
图10-25 云团尺寸—时间曲线
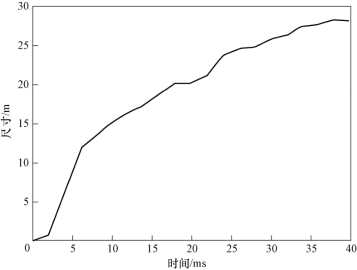
图10-26 云团体积—时间曲线
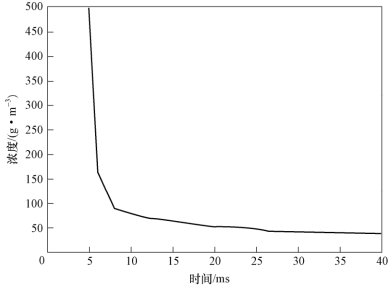
图10-27 云团平均浓度—时间曲线
由以上图可知,采用缩比抛撒装置形成的燃料云团呈宽高相近的圆柱状,云团尺寸和体积随时间逐渐增大,平均浓度相对减小,但是变化速度呈现明显的先快后慢变化,可以据此将云雾扩散过程分为两个阶段:快速沉降阶段和稳定扩散阶段。对试验中获得的超声衰减数据进行滤波处理,数据曲线如图10-28所示。
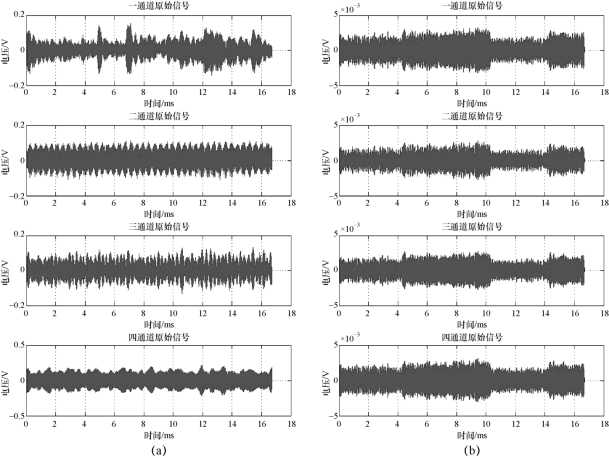
图10-28 典型数据曲线(3号试验数据)
(a)原始数据;(b)滤波数据
根据试验获得的原始数据提取特征参数提取,如表10-6所示。
表10-6 原始数据特征参数表
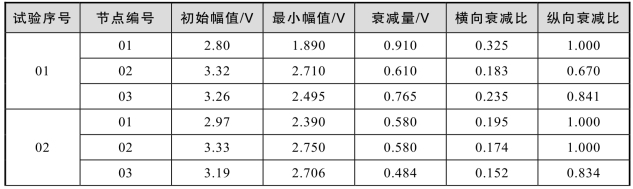
续表

根据原始数据计算云雾浓度,得到广域动态燃料云雾浓度时间变化曲线,如图10-29~图10-31所示。
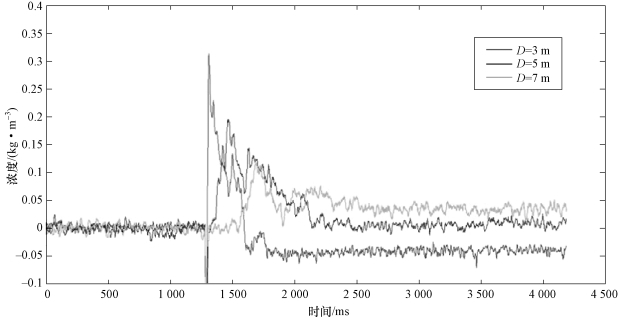
图10-29 试验1 浓度时间变化曲线(彩图见附录)
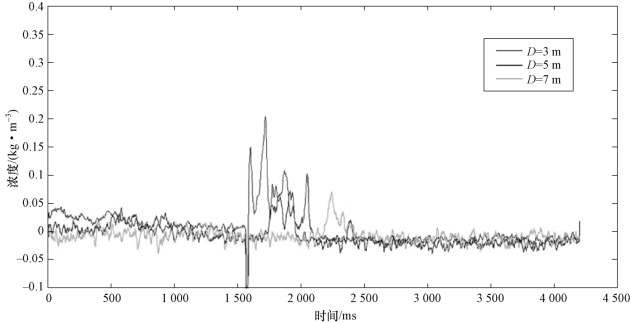
图10-30 试验2 浓度时间变化曲线(彩图见附录)
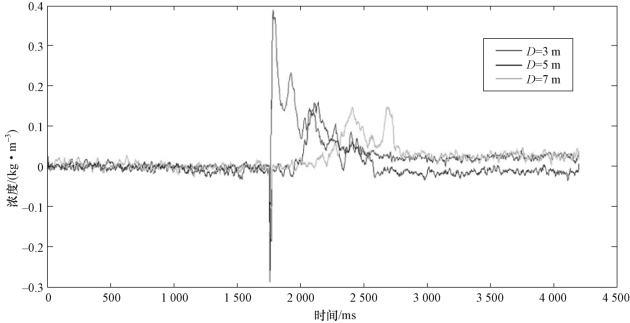
图10-31 试验3 浓度时间变化曲线(彩图见附录)
对以上浓度数据图表进行分析,可以获得以下结论:
(1)各个测试点燃料云团浓度均表现出先增大后减小的趋势,峰值出现时间随测试节点与爆炸中心距离增大而增大,以类似燃料环滚动方式扩散。
(2)在不同测试点,浓度峰值及浓度变化速度随测试节点与爆炸中心距离增大而减小,本次试验中各点浓度峰值比为10:6:4。
(3)云雾抛撒12ms后,01号节点处云雾浓度小于02号和03号节点处的云雾浓度,即云雾分布呈现外高内低的趋势,符合抛撒理论中关于燃料“空洞”现象的描述,可以认为该时刻形成了“空洞”。
