5.2.2 云雾浓度计算模型
对成分已知的混合物浓度进行检测时,电容器输出量(感应电荷)与混合物浓度唯一相关,这一关系体现为混合物等效介电常数计算模型,因此建立合理的混合物等效介电常数计算模型是实现电场法浓度检测的核心技术。然而,对于混合物的等效介电性能,强烈地依赖所含成分的介电常数、体积分数、晶粒形状和空间分布等多项因素,各项因素间存在强度不一的耦合关系,因此混合物等效介电常数计算模型一直是材料学、电子学的研究热点和难点。
早期研究中将混合物视为多种成分的物理混合,通常假设介质由多种不同物质的颗粒均匀地混合而成;颗粒是各向同性的,混合物整体也显示出各向同性,混合物各成分的介电常数之差小于它们本身的介电常数。在上述假设条件下,根据电动力学相关机理,采用数学推理方法建立介电常数计算模型,典型模型包括朗道积分模型和立方根相加模型。
朗道积分计算模型:
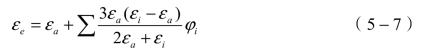
立方根相加模型:
![]()
式中,εe为待求混合物等效介电常数;φi为第i种成分的体积分数;εi为第i种成分的介电常数。
由于上述模型对于混合物颗粒物的电特性和介电常数范围均有较为严格的要求,计算模型与试验结果的匹配度较差,因此使用范围较窄。
当前针对混合物介电特性的研究主要基于有效介质理论。有效介质理论的主要思想是把整个混合介质看成单一介质,具有单一有效介电常数,采用有效介电常数来表征复合介质的介电性质。常用的有效介质理论有:①弥散微结构与Maxwell-Garnett理论;②对称微结构与Bruggeman自洽理论,也称为有效介质理论(EMT);③双团簇微结构与Shen-Ping理论;④级联微结构与微分有效介质理论。
Maxwell-Garnett计算模型:
![]()
式中,εe为待求混合物等效介电常数;εi为分散颗粒的介电常数。
Bruggeman计算模型:
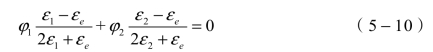
式中,εe为待求混合物等效介电常数;φi为第i种成分的体积分数;εi为第i种成分的介电常数,且有φ1+φ2=1。
相对于传统模型,基于有效介质理论的计算模型对于混合物组成类型及各成分介电特性的限制降低,与仿真和试验结果具有良好的一致性,在吸波材料等研究领域得到了广泛应用和认可。
