2.3.2 陈述式建模
对于一个物理系统而言，各组成部分内部及各组成部分之间的物理关系本身并没有因果性，因此，模型中应当是对模型行为自然描述而无须考虑计算顺序。这种基于方程的建模方式称为陈述式建模，又称为非因果建模，与之相对的是过程式建模或因果性建模。
Modelica是基于方程的建模语言，在上述类型定义中可以看到，中间有明确的行为区域用于以方程来描述模型行为，作为对陈述式建模的补充，Modelica同时支持过程式建模方法。
2.3.2.1 方程与赋值
陈述式建模的特点之一是通过方程而非赋值来描述模型行为。Modelica支持陈述式/过程式混合建模，分别以equation和algorithm来描述方程和赋值，区别在于，equation定义的方程组间的求解顺序将由软件推断确定，而algorithm定义的则按照定义顺序进行求解。例如：
陈述式建模的最大优点是：用户建模时，只需专注于物理问题的陈述，而无须考虑物理问题错综复杂的求解过程怎样实现，因而建模更加简单，所建模型更加健壮。
又例如：在指定力作用下做平面运动的物体可由下述模型类描述。
其中，flange_a与flange_b表示模型的两个接口，又称为连接器，定义如下：
对于模型MovingMass，在已知作用力与已知位移两种情况下，均可以利用该模型来描述，相应约束关系可通过其实例的接口设定，比如：
对于物理系统的各组成部分之间的耦合关系，可以通过与之相对应的模型组件之间的连接来表示，例如：
上述连接语句表示，在ma1的接口flange_a与ma2的接口flange_b之间存在连接。这种连接关系实质上可以转换为如下两个方程，因而也是非因果的。
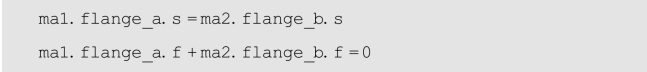
对一个物理系统而言，其各组成部分内部及各组成部分之间的物理关系本身就是非因果的，这与Modelica语言倡导的陈述式建模理念是完全吻合的。
2.3.2.2 连接图与方块图
方块图（又称信号图/框图）是指有数据流向的建模方式，连接图建模方式则与之相对，无须定义数据流向。
多数通用仿真软件，如ACSL、Simulink等，都假定一个系统可以被转换为具有因果关系的结构图，这就意味着以显式状态空间的形式表示模型内各子模型间的相互关系。
以Simulink中一个简单电动机驱动模型为例，如图2-6所示。电动机驱动模型的控制部分在Simulink中很容易理解，而模型中的变速箱、惯量、电动机和负载等部分则不够直观，像变速箱的行为被推导成了方块图中的增益系数1/（J1+Jm*n^2），直接导致方块图无法反映实际物理系统的拓扑结构。
方框图的局限性在于，其模型从输入到输出之间的数据流是单向的。这是导致上述变速箱之类的模型不能被直接描述的原因。另外，如果直接使用基本方程描述而进行仿真，将容易产生代数环。而将方程形式转换为满足Simulink的形式需要用户进行手动分解，带来了不必要的麻烦。
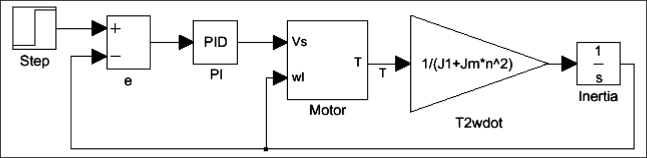
图2-6 Simulink中的简单电动机驱动模型
Modelica支持陈述式建模，通过其面向对象的特性定义模型接口，能够实现直观的连接图和方块图混合建模的方式。组件通过连接机制相互连接在一起，保证组件之间的通信，维护连接之间的约束；非因果组件构成的系统的数据流向由软件自动推导，而因果式组件的数据流向则是显而易见的。
基于Modelica建立的电动机驱动模型，其连接图的建模方式更简捷，也更能够清晰地体现物理系统的实际拓扑结构，如图2-7所示。
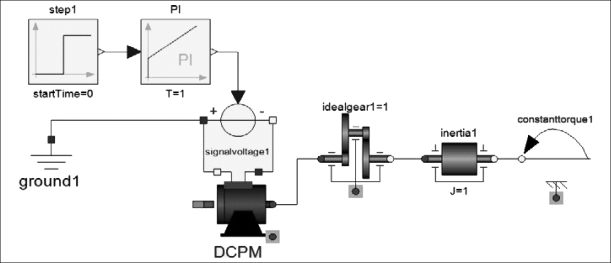
图2-7 基于Modelica的简单电动机驱动模型