3.1.2 硅太阳电池
硅太阳电池的基本结构纵剖面图如图3-4所示。硅太阳电池的基体材料为一薄片p型单晶硅，上表面为一层n+型的顶区，从而构成一个p-n+结。顶区表面有栅状的金属电极，背表面为金属底电极。上、下电极分别与n+区和p区形成欧姆接触，整个上表面还均匀覆盖着减反射膜。
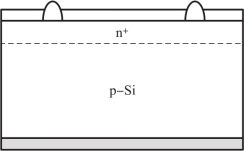
图3-4 n+/p硅太阳电池的基本结构
硅太阳电池被照明时，能量大于硅禁带宽度的光子穿过减反射膜进入硅中，在n区、耗尽区和p区中激发出光生电子-空穴对。光生电子-空穴对在耗尽区中产生后，立即被内建电场分离，光生电子被送进n区，光生空穴则被推进p区。根据耗尽近似条件，耗尽区边界处的载流子浓度近似为零，即p=n=0。在n区中，光生电子-空穴对产生以后，光生空穴便向p-n结边界扩散，一旦到达p-n结边界，便立即受到内建电场的作用，被电场力牵引做漂移运动，越过耗尽区进入p区，光生电子（多子）则被留在n区。p区中的光生电子（少子）同样先扩散、后漂移而进入n区，光生空穴（多子）留在p区。如此在p-n结两侧形成了正、负电荷的积累，产生了光生电压，即光生伏特效应。当光电池接上负载后，光电流就从p区经过负载流至n区，负载中即得到功率输出。硅太阳电池的等效电路如图3-5所示。
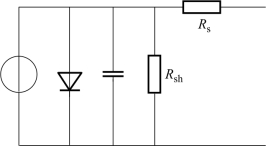
图3-5 硅太阳电池的等效电路图
无光照下的硅太阳电池，与一般的二极管一样，由一个p-n结构成，因此其具有类似二极管的特性。在外电压作用下，p-n结内有一个从p区到n区的二极管单向电流，称为暗电流Id。当有光线照射到太阳电池表面时，在p-n结内产生一个由n区到p区的光生电流IL。IL和Id的方向相反，并且同时存在。硅太阳电池本身是有电阻的，它包括串联电阻Rs和并联电阻Rsh。Rs由上下电极的欧姆接触电阻、硅片n区或者p区的体电阻以及扩散层的薄层电阻等组成，一般是小于1 Ω的电阻。Rsh由p-n结的漏泄电阻和电池边缘的漏泄电阻等组成，一般为几千欧。硅太阳电池还有由p-n结形成的结电容和其他分布电容。由于太阳电池是直流设备，通常没有高频的交流分量，因此这些电容可以忽略不计。根据以上等效电路模型，可以列出方程如下：
式中
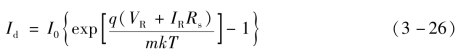
上述方程中的其他变量如下：I0为p-n结反向饱和电流；q为电子电荷，1.6×10-19C；k为玻尔兹曼常数，1.38×10-18erg/K或者0.86×10-4eV/K；T为绝对温度；m为二极管因子常数。
上述方程式是基于物理原理的最基本的解析表达式，已被广泛应用于太阳电池的理论分析中。但是由于表达式中IL、I0、Rs、Rsh，m这5个参数与电池的温度及日照强度有关，在实践中确定十分困难，电池的供应商一般也难以在电池出厂时给出这些参数，因此不便于工程应用。
工程用模型强调实用性与精确性的结合，因此，在进行复杂系统仿真时，需要尽可能在工程精度允许的条件下简化模型。与五参数模型相比较，在工程中可以更方便地得到太阳电池的短路电流Isc、开路电压Voc、最大功率点的电压Vm、电流Im和功率Pm。因此，硅太阳电池的工程用模型要求仅使用以上参数，在一定的精度下尽可能复现太阳电池阵列的特性，并能便于计算机分析。
以下将在上述基本解析表达式的基础上，通过两点近似得到工程用模型，两点近似假设为：
（1）忽略（VR+IRRs）/Rsh项，因为在通常情况下，此项远小于光电流。
（2）假设IL=Isc，这是因为在通常情况下，Rs远小于二极管正向导通电阻。
根据以上假设，太阳电池的I-V方程可以简化为
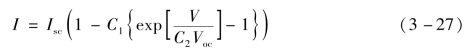
在最大功率点时，V=Vm，I=Im，可得到
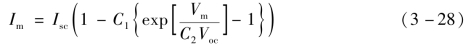
由于在常温条件下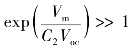
，因此，可以忽略式中的“-1”项，解出C1为
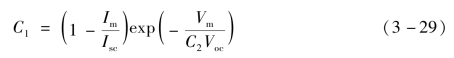
注意到开路状态下，当电流I=0时，电压V=Voc，并把解出的C1代入得到
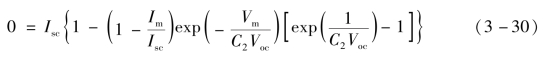
由于
，忽略式中的“-1”项，解出C2得到
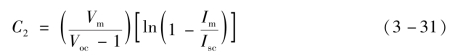
根据以上原理，工程用模型只需要输入太阳电池通常的技术参数Isc、Voc、Im、Vm，就可以根据式（3-29）、式（3-31）得到参数C1和C2，从而根据式（3-27）得到太阳电池的I-V特性。若把太阳电池组件作为二端元件，由于太阳电池组件具有与单体太阳电池类似的特性，因此，按单体太阳电池推导的工程用表达式同样适用于太阳电池组。应用本节所述模型复现太阳电池组件或阵列的I-V特性曲线时，仅需给定生产厂商给出的组件参数，即Isc、Voc、Im、Vm，这将为光伏系统在工程精度下的仿真研究和开发带来极大的方便。其精度可以控制在6%的范围内，这和世界上大部分太阳电池生产厂商所提供太阳电池组件的参数允许波动范围是相适应的。