3.4.3 典型负载模型
负载是指连接在电路中的电源两端,把电能转换成其他形式的能量的装置。电动机能把电能转换成机械能,电灯泡能把电能转换成热能和光能,扬声器能把电能转换成声能。电动机、电灯泡、扬声器等都叫作负载。
根据负载阻抗定义,负载可分为阻性负载、容性负载、感性负载等。
(1)阻性负载:当负载电流与负载电压没有相位差时,负载为阻性负载。
(2)容性负载:当负载电流超前负载电压一个相位差时,负载为容性负载。
(3)感性负载:当负载电流滞后负载电压一个相位差时,负载为感性负载。
要深入理解阻性负载、容性负载和感性负载,需要了解电阻、电容和电感的特性以及有功功率和无功功率。
电阻是描述导体导电性能的物理量,用R表示。电阻由导体两端的电压U与通过导体的电流I的比值来定义,即R=U/I。纯电阻电路是用代数方程来描述的,这就意味着:如果外施的激励源(电压源或电流源)为常量,那么在激励作用到电路的瞬间,电路的响应也立即为某一常量。电阻电路在任一时刻t的响应只与同一时刻的激励有关,与过去的激励无关。因此,电阻电路是“无记忆的”,或者说是“即时的”,而且负载电阻上的电压和电流没有相位差。
设电容如图3-43所示,并且电流i(t)的参考方向箭头指向标注q(t)的极板,这就意味着当i(t)为正值时,正电荷向这一极板聚集,因而电荷q(t)的变化率为正。于是有
![]()
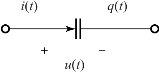
图3-43 电容元件的符号
式中,q为电容的电荷。
又设电压u(t)和q(t)参考方向一致,则对线性电容,得
![]()
式中,C为正值常数,称为电容。
将式(3-88)代入式(3-89),得(https://www.daowen.com)

这就是电容的电压与电流的关系式。显然,这一公式在u和i参考方向一致的情况下才能使用。
对式(3-90)进行拉普拉斯变换,将时域变量转化为频域变量,结合频域知识可知,负载电容的电流超前电压90°。
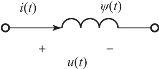
图3-44 电感元件的符号
线性非时变电感元件的磁链ψ与电感L满足
![]()
根据电磁感应定律,感应电压等于磁链的变化率。当电压的参考方向与磁链的参考方向一致,符合右手螺旋法则时,可得
![]()
若电流与磁链的参考方向符合右手螺旋法则,则可将式(3-91)代入式(3-92),得

这就是电感的电压与电流的关系式。显然,这一公式在u和i参考方向一致的情况下才能使用。
与对电容的处理方法一致,对式(3-93)进行拉普拉斯变换,将时域变量转化为频域变量,结合频域知识可知,负载电感的电流滞后电压90°。
由上述知识可知,电阻、电感和电容的负载电压与负载电流的相位差是完全不同的。而且,电阻是有电压就一定有电流;电容是电压变化才有电流;电感则是电流变化才有电压。
电阻、电容和电感是负载的基本组成单元,负载往往是由其单个或是多个组合而成。正是由于三者的电压和电流的相位差不同,导致负载呈现不同的性质,根据整体的负载电压和负载电流的相位关系,一般可分为阻性负载、容性负载和感性负载。
负载元件的阻抗是电路中电阻、电感、电容对交流电的阻碍作用的统称,是频率的函数。感抗和频率成正比,容抗和频率成反比,所以频率可以影响电路的性质。实际电路中,若容抗比感抗大,电路呈容性;若感抗比容抗大,电路呈感性。
