3.2.1 蓄电池建模基础
蓄电池建模是通过数学形式对电池的各项特性进行精准刻画,以实现对电池内部隐含状态和特性的显现表达,从而为这类强时变性非线性系统高精度数字化仿真奠定基础。
3.2.1.1 蓄电池常用建模方法
随着锂离子电池技术的突破,空间用蓄电池已逐步从镍氢、镍镉电池迈进锂离子电池时代,电池的比能量、比功率、循环寿命以及成本都发生了重要变化。但是,电池技术的革新并没有改变蓄电池本身强非线性、强时变性以及对工作温度敏感的三点属性。因此,在电池建模过程中,应考虑电池的电特性、热特性以及老化特性。基于此,蓄电池建模方法可以大致分为4类:①用于描述电池电学属性的电性能建模方法;②用于描述电池充放电过程中电池产(放)热的热特性建模方法;③面向电-热耦合效应的电热耦合建模方法;④描述电池老化特性的老化模型。而其中电性能建模又可以细分为机理分析法、等效电路法和数据驱动法三类。
1)机理分析法
机理分析法是从电池内部反应机制出发,利用多孔电极理论,构建描述电池内部电化学动力学信息的完整方程,从而实现对电池工作过程的精准描述。这种建模方法不但能够准确反映电池外特性(电压和电流)变化,还可以准确反映电池内部微观物理量(电解液过电势、固相锂离子浓度等)的分布和变化情况。通过机理分析法构建的蓄电池模型称为电化学模型,最早的电化学机理模型是由Doyle、Fuller和Newman等人开发的伪二维(Pseudo-2-Dimensional,P2D)模型,该模型由6组方程构成,其中描述粒子在电极和电解液中的扩散效应由偏微分方程构建,这就使得该模型复杂度成倍增加。即便电化学机理模型能够准确反映电池的内外特性变化,但是其复杂度以及模型参数难以获取,大大降低了该模型实时应用的可能。因此,这种建模方法的应用场景主要是面向对实时性要求不高的离线分析、健康状态评估以及缓变形故障预测等。美国A&M大学应用该方法对NASA部分型号(TOPEX、EUVE、UARS和GRO等)空间用蓄电池性能进行在轨分析,取得了一定的成效。
2)等效电路法
等效电路法的建模机制是利用一系列电路元器件按照特定的拓扑进行组合,从而实现对电池外特性的模拟和追踪。按照对时域或者频域信号的模拟,又可以将等效电路模型划分为常规等效电路模型和分数阶阻抗模型。目前,最为常见也是电池管理系统应用最多的就是常规等效电路模型。相比于通过机理分析法建立的机理模型,通过等效电路法构建的模型具备结构简单、模拟精度高、实时性好的特点,能够有效模拟宽工作温度范围、长寿命周期内电池的工作特性。随着星载芯片运算能力的不断提升,未来利用等效电路法对电池建模并将相关算法写入控制器对电池组状态进行实时评估的解决方案是大势所趋,等效电路法将迎来其在空间领域的重要应用前景。但是,这种建模方法的弊端同样应当被重视,那就是由于模型面向对电池外特性的模拟而忽略了电池本身机理性变化,因此,该类模型的物理化学意义远逊于通过机理分析法建立的电化学模型。所以,从电池外特性改变反推电池机理变化,从而约束或者限定模型参数的变化范围和趋势,是应用等效电路模型的关键。
3)数据驱动法
数据驱动法是利用神经网络、深度学习抑或是支持向量机等优化方法构建模型,并通过拟合不同工况下的测试数据训练模型参数,进而得到电池输入/输出特性的非线性模型的方法。该方法对于强非线性、强时变性系统具有较高的拟合精度,因此适用于蓄电池建模过程。但是,利用该方法建模对于训练模型的数据集“质量”要求较高,训练数据应当能够覆盖电池尽可能多的性能信息,否则模型不能全方位反映电池的整体特性,会使电池在一些特殊条件或者工况下失效。另外,“质量”高的数据集意味着需要开展丰富的地面试验,无形之中增加了建模成本,并且模型本身由多种非线性函数组成,结构复杂,计算成本高,不利于嵌入式设计。最后,由于此种建模方法是通过纯数据拟合方式进行建模,模型结构和参数变化缺少物理化学意义解释,因此,模型对电池机理的变化解释能力弱,不适用于电池机理分析。
3.2.1.2 蓄电池常用模型
1)电化学模型
电化学模型是通过机理建模方法构建的一类准确描述电池内部电化学反应的数学模型。常见的电化学模型有伪二维模型、单粒子模型以及简化的伪二维模型等。利用电化学模型不仅能够准确地追踪电池端电压特性,同时,电池内部隐含变量的变化也能够一目了然,便于对电池进行机理分析。最早的电化学模型是由Newman提出的伪二维模型,它由一系列偏微分方程构成。以P2D模型为例,该模型由6组方程构成:描述锂离子活性颗粒半径方向分布的固相锂离子浓度扩散方程、描述固相沿x轴方向的电势分布的固相欧姆定律方程、描述液相沿x轴方向的电势分布的液相欧姆定律方程、描述发生在活性颗粒表面的化学反应速率的Butler-Volmer方程以及电荷守恒方程,具体方程形式见式(3-40)~式(3-44)。
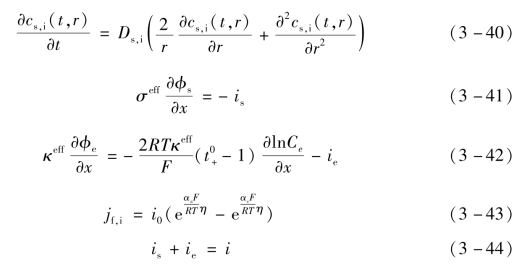
由于电化学模型复杂,无法获得精确的解析解,需要借助数值计算方法求解,常规的求解方法有有限差分法和有限元法。例如,商业软件COMSOL便是利用有限元法对电池模型进行求解。但是,数值计算方法在离散过程中计算量大,不适合与先进控制算法结合实现锂离子电池的状态估计。因此,许多简化求解偏微分方程的方法被应用于P2D模型的简化求解中。即便经过简化,电化学模型的复杂度依旧不能满足嵌入式电池管理系统对模型实时性的高要求,或者为了达到实时性,对控制器的计算能力提出了极高的要求,无形中也增加了电池管理系统的成本。(https://www.daowen.com)
2)等效电路模型
通过等效电路方法建立的等效电路模型则可极大地弥补电化学模型在实时性上的不足。等效电路模型通过一系列电子器件的组合来准确刻画电池的外特性。常规的等效电路模型包括Rint模型、n阶RC模型、阻容模型、PNGV模型等。模型拓扑如图3-12所示。
3)黑箱模型
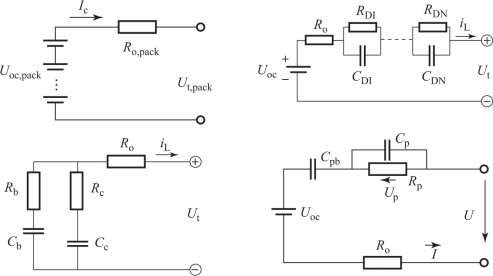
图3-12 蓄电池等效电路模型
由数据驱动方法构建的模型即黑箱模型。该模型不追求对电池内部机理变化的解释,也不需要依托电气元件对电池电压特性进行模拟,而是通过数据、基函数、权重、学习等逼近电池的输出特性。常见的黑箱模型有神经网络模型、支持向量机模型和极限学习机模型等。以径向基函数网络(Radial Basis Function Network,RBF)为基础所建立的黑箱模型包含输入层、隐含层和输出层,其中隐含层激活函数可选用高斯基函数,如下式:
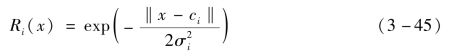
式中,x为n维输入向量;ci为第i个隐含层神经元的高斯基函数中心,当输入信号位于隐含层神经元基函数的中心时,其输出具有最大值。径向基函数网络的输出层是隐含层神经元输出的线性组合,即

式中,R表示输出层节点数;wij表示隐含层到输出层的权重。
评价黑箱模型准确度的标准是电池端电压的误差平方和最小。
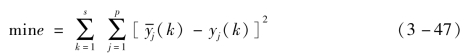
式中,![]() 表示k时刻第j层模型输出。
表示k时刻第j层模型输出。
黑箱模型可以很好地描述电池的外特性,即输入/输出特性,但是缺乏对电池机理的解释。同时,由于模型结构复杂,模型精度取决于训练数据和所选基函数的“质量”。因此,该类模型同样很难写入控制器中进行实时计算。
