5.6.4 模型修正
5.6.4.1 数据驱动的模型动态修正方法
现有模型验证一般依赖调节参数,得到仿真模型的输出响应与真实物理系统的试验数据对比,通过最小二乘或优化方法获得模型的最佳参数。然而,如果一个模型结构存在缺陷,那么通过调整模型参数无法使得其输出响应与真实响应趋于一致。针对常规依赖调节参数开展模型验证方法的不足,采用数据驱动的模型动态修正方法,通过动态响应曲线逼真度度量方法面向模型结构(粗调)和参数(细调)的同步验证,在对地面测试海量数据分析的基础上,使之与在轨飞行真实系统输出趋于一致,提高模型置信度,如图5-21所示。
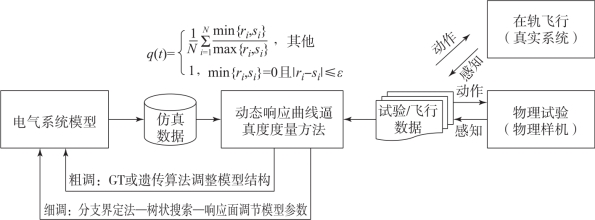
图5-21 实时数据驱动的电气系统模型动态修正技术
1)粗调阶段
对研究对象的模型结构进行调整,实际上就是从模型库中挑选适当的同类模型进行组合,通过一定的方法使组合的结果达到最优效果。于是,对模型结构进行调整可以转化为不同类子模型之间的组合优化问题。组合优化的目标是寻找最优的子模型组合方案,使研究对象的模型整体仿真结果与实际物理系统的真实输出间的差值最小。在时间序列上对仿真结果和实际物理系统的真实输出进行离散,则最小化两者之间的差值即优化目标,见式(5-1)。

式中,Si代表仿真结果;Ri代表实际物理系统的真实输出结果;N代表时间序列的离散数。
2)细调阶段
当粗调阶段完成后,细调阶段则针对模型参数进行调整优化。优化的目标仍然是最小化仿真结果与实际物理系统输出值的差值。复杂电气系统模型通常会同时包含离散型和连续型两种类型的参数变量,针对其构造的优化问题是一个混合离散优化问题,见式(5-2)。
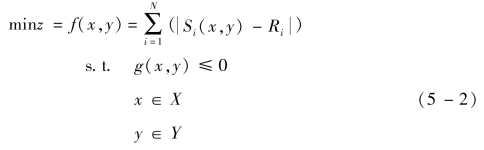
式中,x为连续型变量;y为离散型变量。
对于该混合离散优化问题,采用分支定界法求解。为得到最优值,对于整数变量,采取树状搜索,在求解过程中,某一支上最先求出的该支上的最优点可当作一个可行解,以此作为比较的标准进行模型修正。由于大型复杂系统中常包含大量连续型变量,并且优化过程本身涉及系统仿真计算,因此模型修正过程需要进行大量的计算迭代。
5.6.4.2 验证流程
模型验证即对一定的仿真目的,证实模型行为特性与系统实际行为特性对比精度满足要求,换句话说,就是证实模型的输入/输出变换有足够的精度代表实际系统的输入/输出变换。模型验证流程如图5-22所示。
仿真模型验证原理上包括两项内容:检测模型与系统的行为特性对比精度;证明此精度满足仿真目的规定的要求。
模型验证方式主要分为:
(1)单元验证。单元验证主要证实所建模型与实际设备相关数据的对比是否满足要求的精度,其验证方法有:①与试验数据进行对比;②与成熟仿真软件对比;③与理论经验对比。
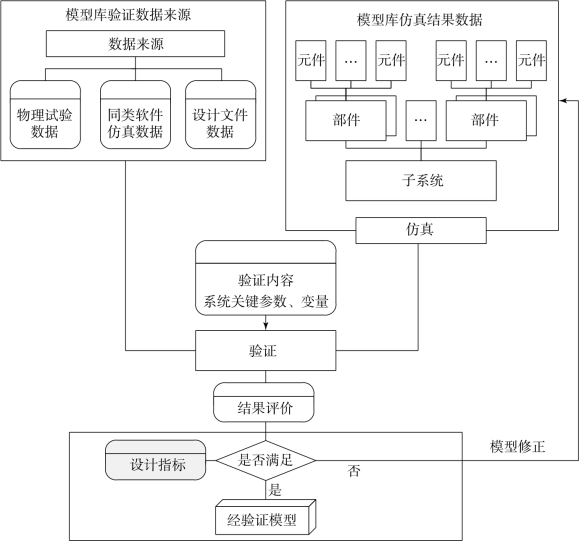
图5-22 模型验证流程
(2)子系统验证。子系统验证相比于单元验证要复杂些,其不再关心单个模型的仿真精度,而是在单元验证的基础上(保证每一个子系统模型的仿真精度在合理范围内)来验证子系统模型各特定指标的精度。
(3)系统验证。系统验证,相比较子系统验证而言,其验证所用的模型数较多且更全面。系统验证可能包含众多领域,是子系统的集合,一般在子系统中能够满足一定的仿真精度,而在多领域系统中不一定能完全满足,因此需要在确认系统验证指标的基础上对系统进行一定的仿真精度验证。
5.6.4.3 数据来源
输入条件的设置原则是尽可能使模型的输入条件与系统工作工况统一,模拟多种形式常值、连续变化的输入信号。
5.6.4.4 结果评价(https://www.daowen.com)
组件模型的测试需得到指定的关键数据结果,并且与对应物理试验结果进行比较。具体结果评价方法可参考静态误差与动态误差评价方式。
1)稳态误差
(1)评价方式。对于稳态误差的评价方法,下面提供几种误差衡量指标:
平均偏差:根据每个采样时刻的仿真值和实际值之间差值的绝对值与仿真值之间的比值来计算误差百分比,最后通过加权的方式获取整批数据的误差。
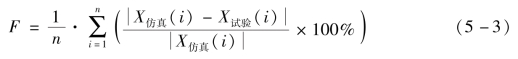
最大误差:所有采样时刻的仿真值与实际值的最大差值。
![]()
(2)应用场景示例。静态误差的使用适用于稳态过程,即系统的输出数据达到一个固定的稳态值时进行评价。其适用于大多数模型的仿真结果评价。
2)动态误差
(1)评价方式。对于动态误差的评价方法,即当输入数据为连续变化,系统的输出数据没有一个固定的稳态值时,无法计算系统输出的稳态误差,此时可考虑以累计误差为评价标准进行衡量。动态过程输入示意如图5-23所示。
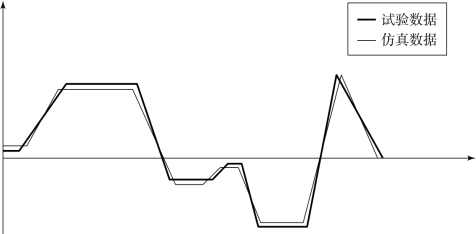
图5-23 动态过程输入示意
累计误差:取试验、仿真曲线绝对值,通过积分的方式计算绝对值曲线面积与各采样点绝对误差曲线面积来反映误差大小,相当于将每个时刻的误差进行累计,如图5-24所示。累计误差计算方式如下:
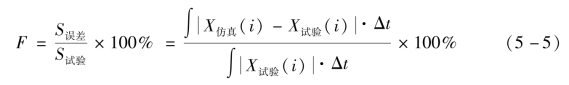
式中,S误差为绝对误差曲线与时间轴所围成的面积;S试验为试验曲线绝对值与时间轴所围成的面积;Δt为采样时间;i为对应每个采样的序号。
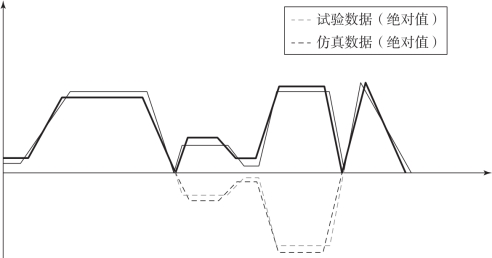
图5-24 累计误差计算示意图
(2)应用场景示例。在如图5-25所示连续变化输入的动态仿真过程中,选择以累计误差评价动态误差的方式比较合适。
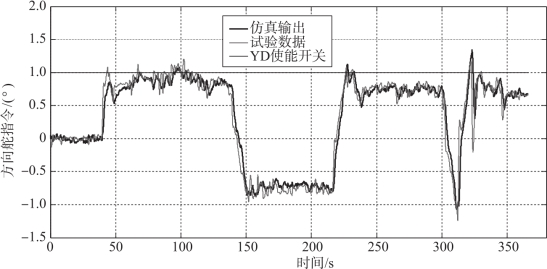
图5-25 基于动态误差的结果评价应用场景
其误差计算结果为:
仿真绝对值曲线面积:239.714 6;
试验绝对值曲线面积:247.052 6;
误差计算:3.06%。
