2.3.3 连续离散混合建模
实际物理模型的动态特性可以是连续时变的,也可以是分段连续时变的,如二极管、物体之间的摩擦力等,还可以是离散时变的,即系统状态只在某些离散时间点上发生变化。动态连续建模的关键是基于能量守恒、动量守恒、质量守恒等基本物理定律来描述系统连续时变行为,而离散事件建模的关键是怎样表达与事件相关的离散行为。
2.3.3.1 同步数据流原理
同步数据流原理是Modelica遵循的基本原理之一,也是解决连续离散混合系统问题的基础。其定义如下:
(1)所有变量保持其实际值,直到这些值被显式改变。变量值可以在连续积分和事件时刻被访问。
(2)在连续积分和事件时刻中的每一时间点,活动的方程表明了变量之间必须同时满足的约束关系(如果if分支、when子句或出现方程的块不是活动的,那么其中所包含的方程也不是活动的),也只有活动的方程才被求解。
(3)在事件时刻的计算和数据通信不计入仿真时间。
(4)方程的总数恒等于未知变量的总数。
利用同步数据流原理处理连续离散混合系统的好处是,连续和离散部分之间的同步自动进行,并且产生没有冲突的确定行为。而且,其他一些方法难以检测的错误,如死锁,往往在翻译期间就可以被检测出来。
基于此,Modelica可兼容其他类似的离散建模方法,如有限自动机、Petri网、状态图和DEVS等,更详细的内容可以参考相关Modelica模型库及其介绍。
2.3.3.2 离散建模方法
Modelica定义的离散变量包括带有discrete前缀的Real变量,Integer、Boolean、enumeration类型的变量。触发事件的符号包括>、<、>=、<=以及内置函数abs()、sign()、div()、mod()、rem()、ceil()、floor()、integer()和initial()、terminal()、sample(),此外,还提供了内置函数noEvent()用于抑制事件的产生。
Modelica语言提供以下两种语法结构用于表达离散模型。
(1)if结构,包含条件表达式和条件方程,用于描述不连续条件模型。(https://www.daowen.com)
(2)when结构,用于表示只在某些离散时刻有效的方程。
if结构的一般形式如下:
![]()
或者

when结构的一般形式如下:

if结构和when结构的区别在于:if结构中的分支方程在分支条件为true的整个区间内都是有效的,变量在整个有效区间内被连续求值;而when结构中的分支方程仅仅在分支条件由false变成true的瞬时生效,变量在事件发生瞬时被求值,并在后续求解过程中保持不变。
图2-8所示的弹跳小球就是一个连续离散混合模型的例子。小球的运动通过球的高度height和速度velocity来描述。小球在两次触地弹起期间连续运动,当接触到地面弹起时,离散事件发生,小球的速度被重置。假定小球的弹性系数为0.9,即每次反弹的速度降为原来的0.9。下面给出模型代码与仿真结果。


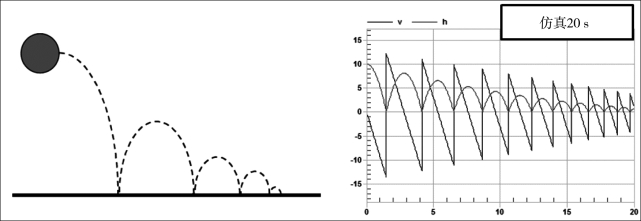
图2-8 弹跳小球及其速度和高度仿真曲线
