3.4.1 开关模型
配电设备中大量电力电子开关的高频工作特性给电磁暂态仿真带来了较大困难。随着开关频率与数量的增加，系统的仿真时间将呈指数级增加。因此，开关模型是影响电力电子系统电磁暂态仿真精度与效率的关键因素之一，通常采用常规或改进的LC等效开关建模法建立开关模型。如图3-34所示，所谓的LC等效开关建模法，是指将导通的开关等效为电感L，关断的开关等效为电容C。
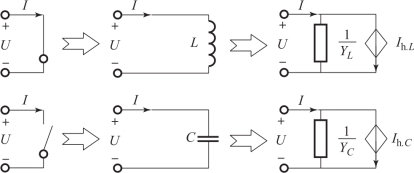
图3-34 经典的LC等效开关建模法
采用Dommel梯形积分法，可以得到图3-34中开关的等效导纳：
式中，Δt为仿真步长；L为等效电感；C为等效电容；YL为导通状态等效导纳；YC为关断状态等效导纳。为了得到恒定的系统导纳矩阵，令YL=YC，因此：
实际使用中，一般通过试凑法或端口阻抗匹配法选取合理的L、C等效参数。
本质上，梯形积分法为基于截断泰勒级数的积分方法，在仿真阶跃响应时容易产生数值振荡问题，增加了等效参数的选取难度。为了解决该问题，如图3-35所示，在等效电路中增加了一对阻值相同、符号相反的虚拟电阻（负电阻用于保持功率平衡），使用指数形式的差分方程（根匹配法）得到一种改进的LC等效开关建模法。
根据图3-35，在开关导通状态下，将RL合并，并根据拉普拉斯变换得到
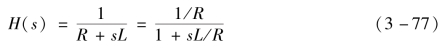
式中，s为复变量；L为等效电感；R为虚拟电阻。根据根匹配法，可得电感电阻串联支路的等效导纳与历史电流，见式（3-78）。
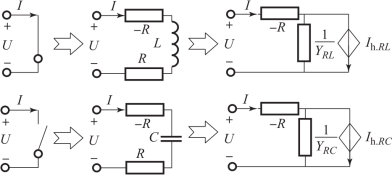
图3-35 改进的LC等效开关建模法
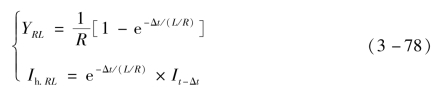
式中，YRL为导通状态等效导纳；Ih.RL为历史电流；It-Δt为上一时步的支路电流；e为自然常数。
在开关关断状态下，将RC合并，并根据拉普拉斯变换得到
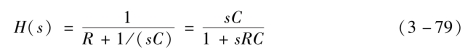
式中，s为复变量；C为等效电容；R为虚拟电阻。根据根匹配法，可得电容电阻串联支路的等效导纳与历史电流，见式（3-80）。
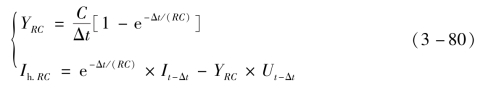
式中，YRC为关断状态等效导纳；Ih.RC为历史电流，Ut-Δt为上一时步的支路电压；e为自然常数。为了保持系统导纳矩阵不变，令YRL=YRC，即
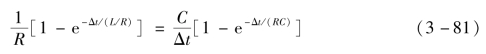
容易得到等效电感、电容参数，见式（3-82）：
从而有
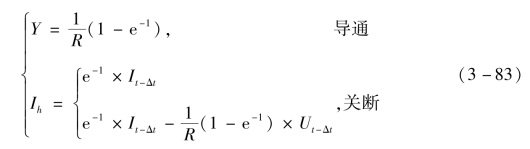
式中，Y为开关的等效导纳；Ih为历史电流。
一般地，式（3-82）和式（3-83）中等效电阻的取值范围为0.01～10 Ω，因此，在确定仿真步长后，可以很容易确定开关的LC等效参数，并得到等效导纳与历史电流。