3.1.1 太阳电池建模基础
太阳电池是利用半导体材料吸收光，产生光生伏特现象的发电器件。在航天领域，发展初期主要采用单晶硅电池作为航天器电源产品，效率为14%～15%，可适应早期小功率的航天器需求。近年来，航天器的功率需求逐步增大，具有高效率的砷化镓系太阳电池技术不断进步，目前三结砷化镓太阳电池的量产效率已近30%，硅太阳电池逐步被砷化镓电池所取代，更高效的砷化镓太阳电池技术迅速发展。
砷化镓太阳电池主要经历了GaAs基系单结太阳电池、GaAs基系双结叠层太阳电池和GaAs基系三结叠层太阳电池。目前的GaAs电池产品主要为三结结构，随着技术的不断成熟以及对新产品的需求，四结或更多结太阳电池、倒装电池、细节叠层和量子阱电池等新技术不断有所突破。
本节首先对太阳电池的基本工作原理及相关模型进行总结，然后针对硅太阳电池、单结GaAs电池和三结GaAs电池三个实例给出工程中常用的建模方法和结果。
1）光电流
光生载流子的定向运动形成光电流。若投射到电池上的光子中，能量大于Eg的光子均能被电池吸收，从而激发出数量相同的光生电子-空穴对，并且均可被全部收集，则光电流密度的最大值为
式中，Nph（Eg）为每秒投射到电池上的能量大于Eg的总光子数。
考虑光的反射、材料的吸收、电池厚度以及光生载流子的实际产生率，光电流密度可以表示为
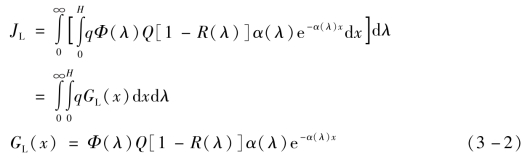
式中，Φ（λ）为投射到电池上、波长为λ、带宽为dλ的光子的个数；Q为量子产额，即一个能量大于Eg的光子产生一对光生载流子的概率，通常可以令Q=1；R（λ）为和波长有关的反射因数；α（λ）为对应波长的吸收系数；dx为距电池表面x处厚度为dx的薄层；H为电池总厚度；GL（x）表示在x处光生载流子的产生率。
这个表达式的前提假设为，凡是在电池中产生的光生载流子，均可对光电流有贡献，因此该表达式是光电流的理想值。根据太阳电池光电流的形成过程可知，在如图3-1所示的简化太阳电池结构中，①太阳电池的n区、耗尽区和p区中均能产生光生载流子；②各区中的光生载流子必须在复合之前越过耗尽区，才能对光电流有贡献，所以求解实际的光生电流必须考虑到各区中的产生和复合、扩散和漂移等各种因素。为简单起见，先讨论波长为λ，带宽为dλ、光子数为Φ（λ）的单色光照明太阳电池的情况。
类似p-n结正偏，在单位面积的太阳电池中，把JL（λ）看作各区贡献的光电流密度之和：
式中，Jn（λ）、JG（λ）、Jp（λ）分别表示n区、耗尽区和p区贡献的光电流密度。在考虑各种产生和复合后，可求出每一区中光生载流子的总数和分布，从而求出电流密度。
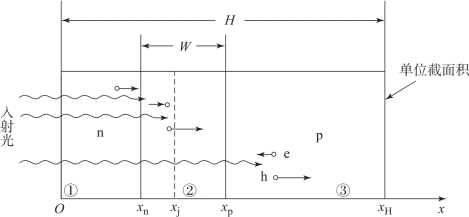
图3-1 计算光电流时所用的太阳电池结构
根据p-n结的理论模型，假设如图3-1所示的太阳电池满足：
（1）光照对太阳电池各区均满足pn＞
，即满足小注入条件。
（2）耗尽区宽度W小于扩散长度L，并满足耗尽近似。
（3）基区少子扩散长度大于电池厚度，结平面为无限大，不考虑周界的影响。
（4）各区的杂质均已电离。
在一维情况下，太阳电池工作状态的基本方程如下：
对n区，有
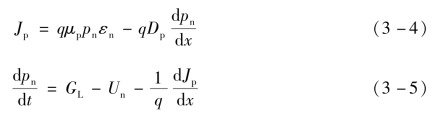
对p区，有
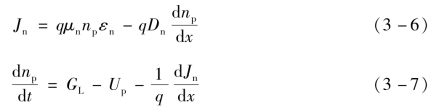
以及
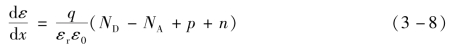
以上5个方程中各个符号的物理意义以及单位为：
Jn，Jp：电子、空穴电流密度（C/（cm2·s））；
nn，np：n区电子、空穴浓度（cm-3）；
pn，pp：p区电子、空穴浓度（cm-3）；
μn，μp：电子、空穴的迁移率（μm2/（s·V））；
Dn，Dp：电子、空穴的扩散系数（cm2/s）；
Ln，Lp：电子、空穴的扩散长度（μm/s）；
τn，τp：电子、空穴的寿命（μs）；
ND，NA：施主、受主的浓度（cm-3）；
q：单位电荷量（C）；
εn，εp：电场强度（n区、p区）（C/cm2）；
εr，ε0：材料的相对、绝对介电系数；
GL：光生载流子产生率（1/（cm2·s））；
Un，Up：复合率（电子、空穴）（1/（cm2·s））。
上述5个方程，第一个为电流密度方程，它表示n区中空穴决定的电流密度等于空穴的漂移分量与扩散分量的代数和；第二个为连续性方程，它表示在单位时间单位体积的半导体中，空穴浓度的变化量等于净产生率（产生率减去复合率）与空穴流密度的代数和，其中末项前的负号表示扩散电流的方向和空穴浓度梯度方向及电流密度方向均相反；第三个方程和第四个方程分别为p区中由电子决定的电流密度方程和连续性方程；第五个方程为泊松方程，它反映了半导体中电势的空间分布和空间电荷的关系。
2）光电压
由于光照在电池两端出现的电压称为光电压。它像外加于p-n结的正偏压一样，与内建电场方向相反，这降低了势垒高度，而且使耗尽区变薄。太阳电池在开路状态的光电压称为开路电压。
有光照时，内建电场分离的光生载流子形成由n区指向p区的光电流JL，而太阳电池两端出现的光电压即开路电压Voc却产生由p区指向n区的正向结电流JD。在稳定光照时，光电流恰好和正向结电流相等（JL=JD）。p-n结的正向电流可表示为
于是有
两边取对数并整理后，当A→1时，得
由于
，所以
由式（3-12）可知，Voc随JL增加而增加，随J0增加而减小，随着曲线因子A增加而增加。实际上，A因子的增加，与J0的增加有关。所以，总的来说，A因子大的电池开路电压不会大。在忽略产生电流影响时，反向饱和电流密度为
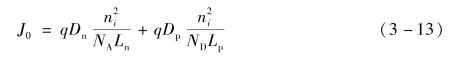
因为
所以
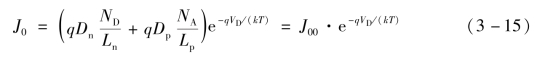
其中
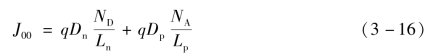
VD为最大p-n结电压，等于p-n结势垒高度，则当A=1时，可得到
在低温和高光强时，Voc接近VD，VD越高，Voc也越大。因为
，所以p-n结两边掺杂度越大，开路电压也越大。把Voc和Eg的比值称为电压因子（V·F），以描述开路电压与禁带宽度的关系，电压因子（V·F）可表示为
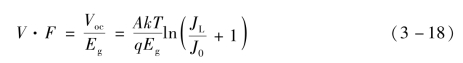
就材料而言，禁带宽度越大，J0越小，开路电压越高。
3）太阳电池输出功率
当受照明的太阳电池接上负载时，光生电流流经负载，并在负载两端建立起端电压，这时太阳电池的工作情况可用图3-2所示的等效电路来描述。图中太阳电池等效为一个能够稳定产生光电流IL的电流源（如果光源稳定），与之并联的有一个处于正偏压的二极管以及一个并联电阻Rsh（也称为跨接电阻）。显然，二极管的正向电流ID=I0[eqV/（AkT）-1]和旁路电流Ish都要靠IL提供，剩余的电流经过一个串联电阻Rs流出太阳电池而进入负载RL。对于实际的太阳电池，可以看作是很多个具有这一等效电路结构的电池单元的并联，因此，图3-2所示的等效电路中，各个参量视为集中参量。
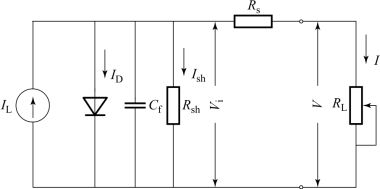
图3-2 p-n结太阳电池等效电路图
当流进负载RL的电流为I，负载的端电压为V时，则
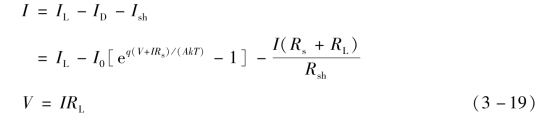
则功率
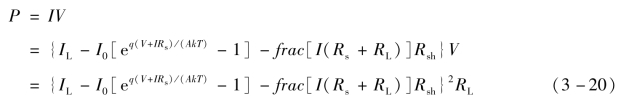
式中，P为太阳电池被照明时在负载RL上得到的输出功率。当负载RL从零变到无穷大时，即可画出如图3-3所示太阳电池的负载特性曲线。
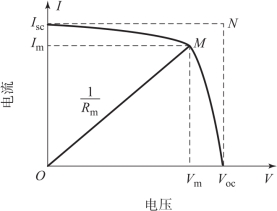
图3-3 太阳电池的负载特性曲线
曲线上的任一点都称为工作点，工作点和原点的连线为负载线，负载线的斜率的倒数即等于RL，与工作点对应的横纵坐标分别为工作电压和工作电流。调节负载电阻RL到某一值Rm时，在曲线上得到的一点M，对应的工作电流Im和工作电压Vm之积最大，即
则M点为该太阳电池的最佳工作点（最大功率点），Im为最佳工作电流，Vm为最佳工作电压，Rm为最佳负载电阻，Pm为最大输出功率。
最大输出功率与（Voc×Isc）之比为填充因数（F·F），也就是图3-3中四边形OImMVm与四边形OIscNVoc面积之比，这个参数是用来衡量太阳电池输出特性好坏的重要指标之一。
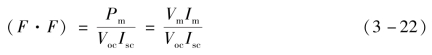
填充因数表征太阳电池的优劣，在一定的光强下，（F·F）越大，曲线越接近矩形，输出功率也越高。（F·F）与入射光强、反向饱和电流、A因子、串联电阻、并联电阻密切相关。太阳电池受照明时，输出功率与入射光功率之比η为太阳电池的效率，即光电转换效率。
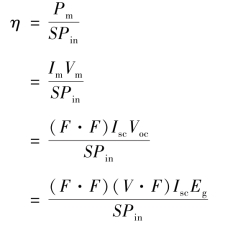
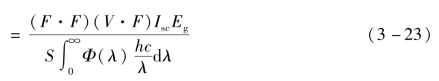
式中，S为太阳电池总面积；
为单位面积入射光功率。