例2 圆管水平斜切的展开
已知圆管直径为40，高为40，截面高为30，求做其展开图。
1.三角形展开法求做圆管水平斜切的展开图
（1）做图思考与分析
1）利用已知条件做出立体图和主、俯两视图（见图2-79）。
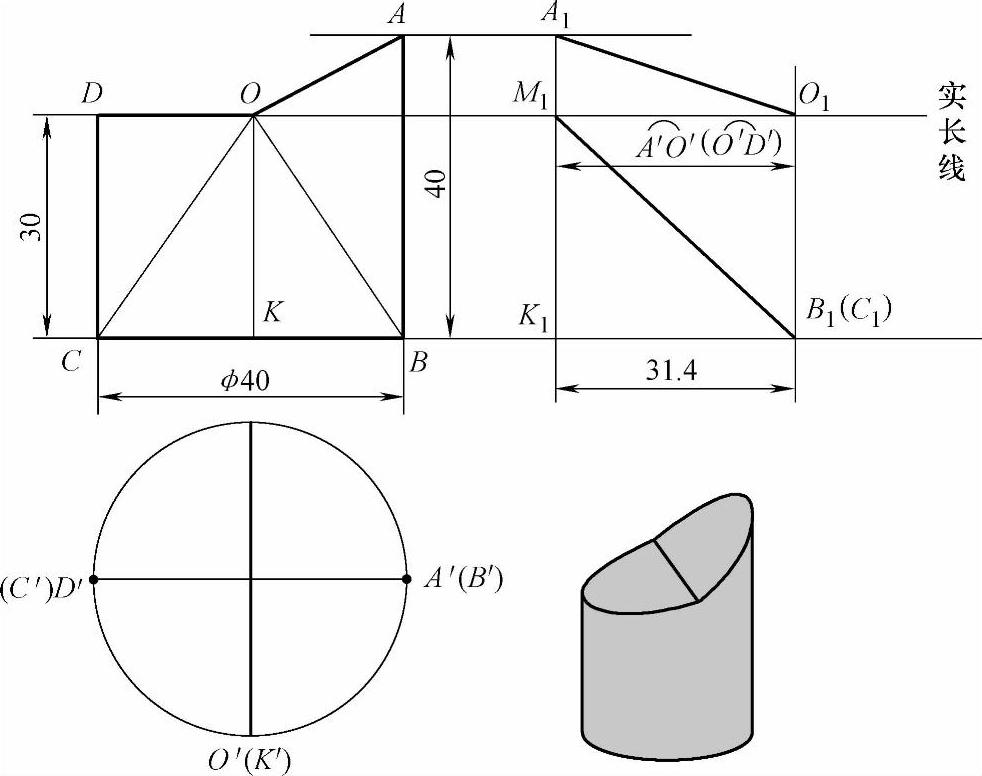
图2-79 圆管水平斜切的立体图、主俯两视图和展开的实长线
2）从立体图和主、俯两视图中看到圆管表面的素线不能共交于一点，所以不适宜用放射线法做展开。
3）如果用三角形法做展开，就得在主视图上至少做两条辅助线，即辅助线CO和BO，这样就把主视图分成三个三角形。
4）求辅助线CO、BO实长的过程如下：①在主视图上向右做圆管底边CB、线段DO的延长线，过圆管斜切线上的A点向右做平行于两条延长线的平行线。②在过A点的平行线上取点A1，过A1点做下垂线，与线段DO延长线交于M1点，与底边CB延长线交于K1点。③以M1点为圆心，以俯视图中A′点至O′点弧线的展开长度（即1/4圆弧=31.4）为半径画弧，与线段DO延长线交于O1点。用线段连接O1点和垂线上的A1点，那么这条线段长就是线段AO的实长线。④因为俯视图中的O′点至（C′）点弧线的展开长度和俯视图中的O′点至（B′）点弧线的展开长度都为31.4，所以以K1点为圆心，以两条弧线展开长度为半径分别画弧，两条弧线与线段CB的延长线相交的交点为同一点，即B1（C1）点。过B1（C1）点做线段与垂线上的M1点相连，那么这条线段长就是主视图上辅助线CO和BO的实长。
（2）展开步骤
1）在适宜位置做主视图线段AB（见图2-80），以线段AB为基准线。以A点为圆心，线段A1O1为半径，往基准线两边画弧；再以B点为圆心，B1M1为半径，往基准线两边画弧，与刚才的两弧分别相交于左右两个O点。过A点分别做线段与两个O点相连，过B点分别做点画线与两个O点相连。
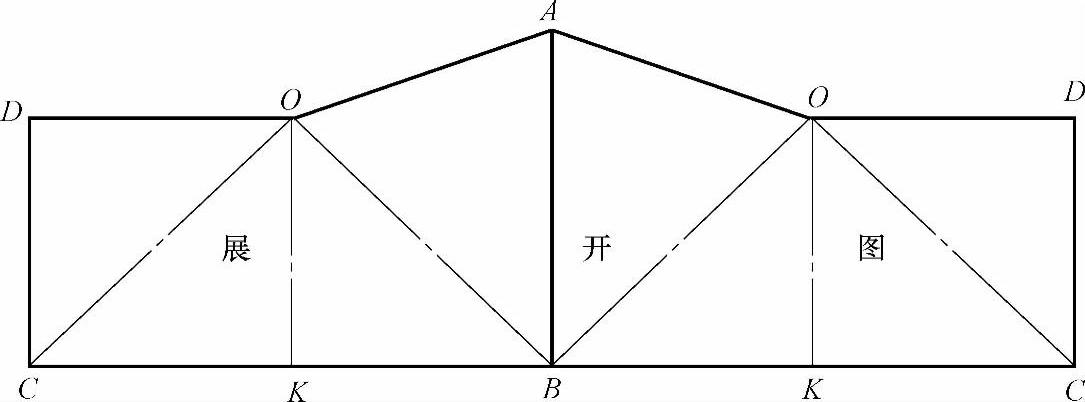
图2-80 用三角形法所做的圆管水平斜切的展开图
2）以B点为圆心，俯视图中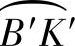
的展开长度（即31.4）为半径往基准线两边画弧；再分别以两个O点为圆心，主视图中线段OK为半径画弧，与刚才的两弧分别相交，得交点为两个K点。过B点分别做线段与两个K点相连，过两个O点分别做点画线与K点相连。
3）分别以两个K点为圆心，俯视图中的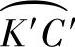
的展开长度（即31.4）为半径画弧；再分别以两个O点为圆心，C1M1的实长为半径画弧，与刚才的两弧分别相交，得交点为两个C点。过C点分别做线段与两个K点相连，做点画线与两个O点相连。
4）分别以两个C点为圆心，主视图中线段CD为半径画弧；再分别以O点为圆心，俯视图中的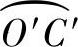
的展开长度（即31.4）为半径画弧，分别与刚才的两弧相交，得交点为两个D点。过两个D点做线段分别与两个O点和C点相连，那么相连后的图形即为圆管水平斜切的展开图。
注：展开图中首尾端点，用同一字母（如C或D）表示，是因为在以展开图的形式对接时，两端点重合为一点（C或D）。后文图中类似情况同此注释。
2.平行线法求做圆管水平斜切的展开
（1）做图思考与分析
1）利用已知条件做出主、俯两视图（见图2-81）。
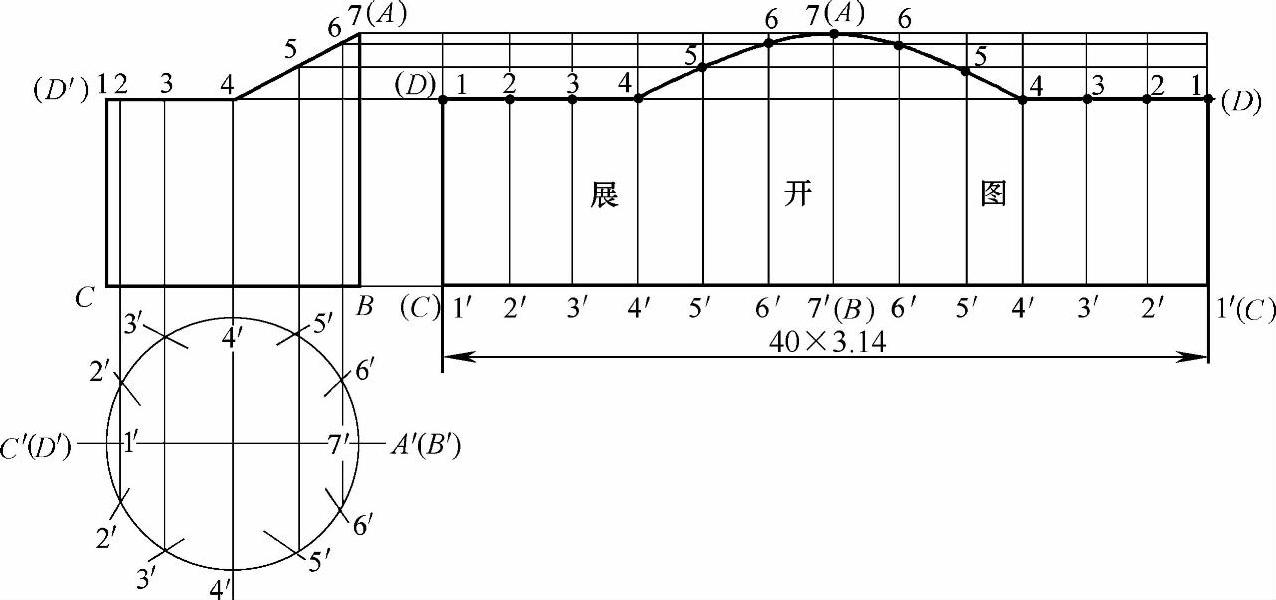
图2-81 用平行线展开法所做的圆管水平斜切的展开图
2）如果用平行线法做展开图，构件表面的素线必须相互平行。从立体图中看圆管表面素线互相平行，所以可以用平行法做展开，即将构件表面分割成若干块相互平行的部分，把它平摊在一个平面上。
（2）展开步骤
1）把俯视图中的圆周十二等分，等分点为1′、2′、3′、4′、5′、6′、7′、6′、5′、4′、3′、2′点，也就是把圆管形体表面分成十二个平行部分。
2）由俯视图上等分点1′、2′、3′、4′、5′、6′、7′点向主视图上引线段BC的垂线，与主视图上水平斜切线交于1、2、3、4、5、6、7点。
3）把主视图圆管线段BC水平向右引延长线，并过主视图水平斜切线上1、2、3、4、5、6、7点向右做平行于线段BC延长线的平行线。在BC延长线上截取长度等于圆管周长的部分，并将其十二等分（因为俯视图把圆管十二等分，所以要对应十二等分），等分点为1′、2′、3′、4′、5′、6′、7′、6′、5′、4′、3′、2′、1′点。过各等分点做延长线的垂线，各垂线与各平行线上对应相交，得各对应交点为1、2、3、4、5、6、7、6、5、4、3、2、1点。
4）用线段连接1、2、3、4点，用曲线圆滑连接4、5、6、7、6、5、4点，连接后的这个图形就是圆管水平斜切的展开图。