例133  圆管60°两节弯头的展开简易法

例133 圆管60°两节弯头的展开简易法

已知圆管直径φ为30，中心弧线R为50，节数为N为2，角度α为60°，求做展开。

思路分析：

因为圆管60°度两节弯头样式一样，所以每节圆管的相贯线（即被切割线）与圆管中心轴线的夹角为60°/2，即30°，可以直接在成管中下料切割，因此中心弧线与角度就可以不必再求做。

展开步骤：

1）做出圆管的垂直投影图，即矩形ABCD（见图2-218）。

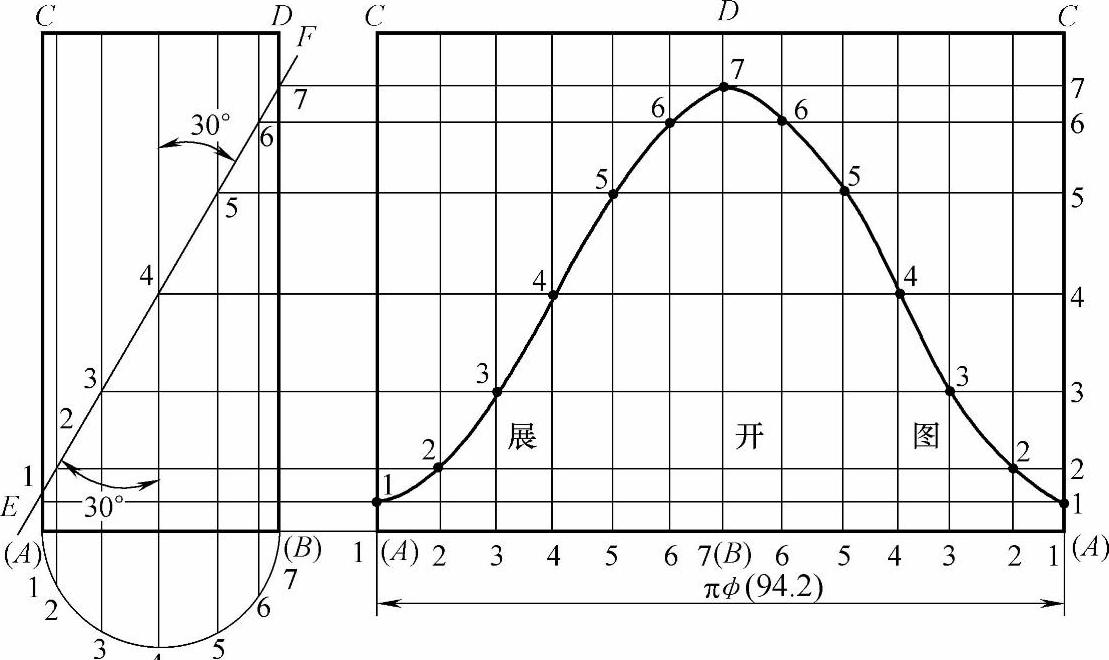
图2-218 圆管60°两节弯头的展开图

2）在圆管垂直投影图中适宜位置做一切割线EF，切割线EF与圆管中心轴线的夹角为30°。

3）在圆管底线段AB上做圆管的半圆，并把半圆六等分，等分点为1、2、3、4、5、6、7点。过1、2、3、4、5、6、7点向上做线段AB的垂线。七条垂线与切割线EF交于点1、2、3、4、5、6、7点。

4）做线段AB、CD向右引的延长线，并过切割线上的七个点做线段AB延长线的平行线。对应在线段AB及CD延长线上截取长等于圆管周长的线段（π×30=94.2）。十二等分线段AB的延长线段，等分点为1（即A点）、2、3、4、5、6、7（即B点）、6、5、4、3、2、1（即A点）。过各等分点做向上做线段AB延长线的垂线，十三条垂线与七条平行线对应相交，得各对应交点为1、2、3、4、5、6、7、6、5、4、3、2、1点。用曲线圆滑连接这些点，即得圆管60°两节弯头相贯线的展开，整个矩形既为圆管60°两节弯头的展开图。