例19  两节任意角度等径圆管弯头的展开

从前述学过的相贯线的性质与特点中得知：等径圆管相贯，相贯线为封闭直线。因此两节等径弯头任意角度的相贯线可直接在主视图中做出。因两节弯头的展开样式一样，所以只需求做出一节弯头展开即可。

1）按已知尺寸画出主视图和相贯线（见图2-101）。

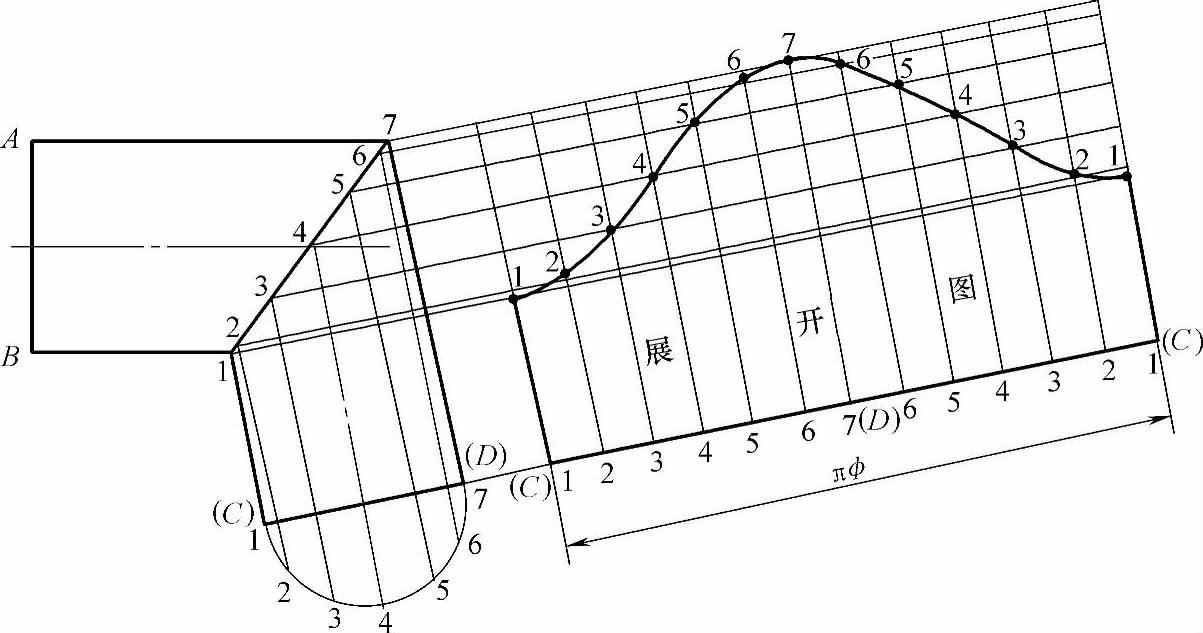
图2-101 两节任意角度等径圆管弯头其中一节的展开图

2）在主视图弯头下端口线段CD的下方做半圆，并把半圆六等分，等分点为1、2、3、4、5、6、7点。过这七个等分点向上做与弯头下端口线段CD的垂线，垂线交弯头相贯线上的点为1、2、3、4、5、6、7点。

3）做主视图线段CD向右引的延长线，在延长线上截取等于圆管周长的线段，并做十二等分，等分点为1、2、3、4、5、6、7、6、5、4、3、2、1点。过各等分点做CD延长线的垂线。

4）过主视图中相贯线上的七个相贯点向右做平行于CD延长线的平行线，平行线与CD延长线上的十三条垂线对应相交，得各对应交点为1、2、3、4、5、6、7、6、5、4、3、2、1点。用曲线圆滑连接这些点，即得到两节弯头中的一节的展开图（另一节与其相同）。